设函数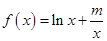 ,
,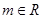 .
.
(1)当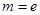 (
(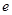 为自然对数的底数)时,求
为自然对数的底数)时,求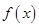 的极小值;
的极小值;
(2)讨论函数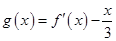 零点的个数.
零点的个数.
某花店每天以每枝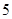 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝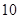 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进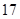 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润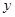 (单位:元)关于当天需求量
(单位:元)关于当天需求量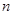 (单位:枝,
(单位:枝,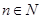 )的函数解析式;
)的函数解析式;
(2)花店记录了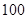 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量 |
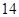 |
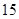 |
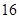 |
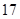 |
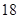 |
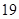 |
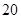 |
| 频数 |
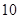 |
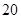 |
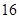 |
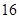 |
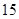 |
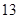 |
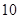 |
①假设花店在这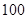 天内每天购进
天内每天购进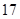 枝玫瑰花,求这
枝玫瑰花,求这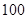 天的日利润(单位:元)的平均数;
天的日利润(单位:元)的平均数;
②若花店一天购进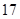 枝玫瑰花,以
枝玫瑰花,以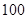 天记录的的各需求量的频率作为各需求量发生的概率,
天记录的的各需求量的频率作为各需求量发生的概率,
【文科学生继续做】 求当天的利润不少于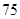 元的概率.
元的概率.
【理科学生继续做】 求当天的利润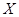 (单位:元)的分布列与数学期望.
(单位:元)的分布列与数学期望.
在 中,内角
中,内角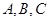 所对的边分别是
所对的边分别是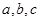 .已知
.已知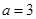 ,
,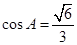 ,
,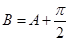 .
.
(1)求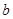 的值;
的值;
(2)求 的面积.
的面积.
已知函数 ,
, .
.
(1)求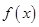 的最小正周期;
的最小正周期;
(2)求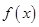 在
在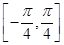 上的最小值和最大值.
上的最小值和最大值.
已知函数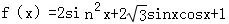 .
.
(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)求f(x)在 上的最值及取最值时x的值.
上的最值及取最值时x的值.