已知数列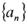 中a1=2,点
中a1=2,点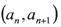 在函数
在函数 的图象上,
的图象上,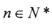 .数列
.数列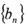 的前n项和为Sn,且满足b1=1,当n
的前n项和为Sn,且满足b1=1,当n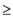 2时,
2时,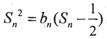 .
.
(I)证明数列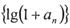 是等比数列;
是等比数列;
(II)求Sn
(III)设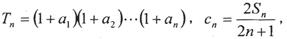 求
求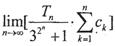 的值.
的值.
如图所示,曲线C由部分椭圆C1: +
+ =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为 .
.
(1)求a,b的值;
(2)过点B的直线l与C1,C2分别交于点P,Q(P,Q,A,B中任意两点均不重合),若AP⊥AQ,求直线l
的方程.
已知Sn是数列{an}的前n项和,且Sn=2an-2n对n∈N*成立.
(1)证明数列{an+2}是等比数列,并求出数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn .
在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
(1)求证:平面PDC⊥平面PAD;
(2)求二面角EACD的余弦值;
(3)求直线CD与平面AEC所成角的正弦值.
已知向量m=(sin ωx+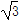 cosωx,1),n=(2cos ωx,-
cosωx,1),n=(2cos ωx,-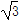 )(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为
)(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为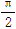 .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈[-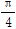 ,
,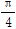 ] 时,求f(x)的值域.
] 时,求f(x)的值域.
已知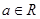 ,命题
,命题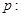 “
“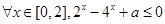 均成立”,命题
均成立”,命题 “函数
“函数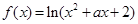 定义域为R”.
定义域为R”.
(1)若命题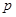 为真命题,求实数
为真命题,求实数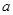 的取值范围;
的取值范围;
(2)若命题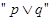 为真命题,命题
为真命题,命题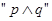 为假命题,求实数
为假命题,求实数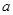 的取值范围.
的取值范围.