已知圆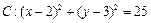 ,直线
,直线 .
. (1)求证:直线
(1)求证:直线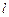 与圆
与圆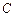 恒相交;
恒相交;
(2)求直线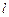 被圆
被圆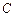 截得的弦长最短时
截得的弦长最短时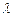 的值以及最短弦长.
的值以及最短弦长.
(本小题满分12分)
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
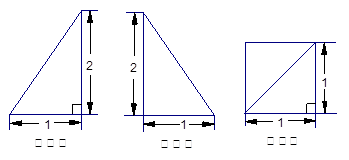
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)当点E在何位置时,BD⊥AE?证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D-AE-B的大小.
(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球中恰有1个红球的概率;
(Ⅱ)设“从甲盒内取出的2个球恰有1个为黑球”为事件A;“从乙盒内取出的2个球都是黑球”为事件B,求在事件A发生的条件下,事件B发生的概率;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
在 中,已知内角
中,已知内角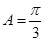 ,边
,边 .设内角
.设内角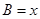 ,
, 的面积为
的面积为 .
.
(Ⅰ)求函数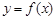 的解析式和定义域;
的解析式和定义域;
(Ⅱ)当角B为何值时, 的面积最大。
的面积最大。
(本小题满分10分)
若关于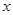 的不等式
的不等式 的解集为非空集合,求实数
的解集为非空集合,求实数 的取值范围。
的取值范围。
(本小题满分10分)
在直角坐标系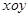 中,直线
中,直线 :
: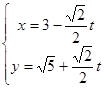 (
(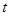 为参数),在极坐标系中(以原点为极点,以
为参数),在极坐标系中(以原点为极点,以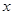 轴正半轴为极轴),圆C的方程:
轴正半轴为极轴),圆C的方程: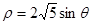
(1)求圆C的直角坐标方程;
(2)设圆C与直线 交于
交于 ,
,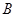 两点,点
两点,点 的坐标
的坐标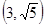 ,求
,求