（本小题满分12分）
已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑球，现从甲、乙两个盒内各任取2个球.
（Ⅰ）求取出的4个球中恰有1个红球的概率；
（Ⅱ）设“从甲盒内取出的2个球恰有1个为黑球”为事件A；“从乙盒内取出的2个球都是黑球”为事件B，求在事件A发生的条件下，事件B发生的概率；
（Ⅲ）设
为取出的4个球中红球的个数，求的分布列和数学期望。
. (本小題满分12分)
已知函数
的图象过点P( 1，2)，且在点P处的切线与直线x-3y=0垂直.
(2) 若
，试求函数f(x)的单调区间；
(3) 若a>0,b>0且（
，m），(n，
）是f(x)的单调递
增区间，试求n-m-2c的范围
(本小题满分12分）
已知椭圆C: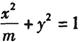
的左、右焦点分别为F1 ,F2，若椭圆上总存在点P,使得点P在以F1,F2为直径的圆上.
(1) 求椭圆离心率的取值范围；
(2) 若AB是椭圆C的任意一条不垂直x轴的弦,M为弦的中点，且满足
(其中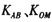
分别表示直线AB、OM的斜率,0为坐标原点），求满足题意的椭圆C的方程.
(本小题满分
12分)
将函数
的图像上各点的横坐标缩短为原来的
（纵坐标不变），再向左平移
个单位后，得到的图像与函数g(x)="sin" 2x的图像重合.
(1) 写出函数y =f(x)的图像的一条对称轴方程；
(2) 若A为三角形的内角，且
•，求
的值
（本小题满分14分）
已知定义在R上的函数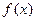
和数列
，当
时，
，其中
均为非零常数．
（Ⅰ）若数列
是等差数列，求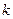
的值；
（Ⅱ）令
，求数列
的通项公式；
（Ⅲ）若数列为等比数列，求函数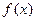的解析式．
（本小题满分13分）
已知椭圆
经过点
，离心率为
，动点
（Ⅰ）求椭圆的标准方程；
（Ⅱ）求以OM为直径且被直线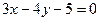
截得的弦长为2的圆的方程；
（Ⅲ）设F是椭圆的右焦点，过点F作OM的垂线与以OM为直径的圆交于点N，证明线段ON的长为定值，并求出这个定值．