如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为m A=20kg,mB=10kg,A、B之间,B与地面之间的动摩擦因数均为μ=0.5,一轻绳一端系住物体A,另一端固定在墙上,绳与竖直方向的夹角为370,今欲用外力F将物体B匀速向右拉出,(取g=10m/s2,sin370=0.6,cos370=0.8)求: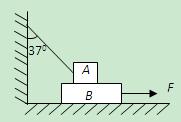
(1)轻绳对A的拉力大小
(2)水平外力F的大小
现代科学仪器常利用电场、磁场控制带电粒子的运动。在真空中存在着如图所示的多层紧密相邻的匀强电场和匀强磁场,电场和磁场的宽度均为d。电场强度为E,方向水平向右;磁感应强度为B,方向垂直纸面向里。电场、磁场的边界互相平行且与电场方向垂直,一个质量为m、电荷量为q的带正电粒子在第1层电场左侧边界某处由静止释放,粒子始终在电场、磁场中运动,不计粒子重力及运动时的电磁辐射

(1)求粒子在第2层磁场中运动时速度 的大小与轨迹半径 ;
(2)粒子从第n层磁场右侧边界穿出时,速度的方向与水平方向的夹角为 ,试求 ;
(3)若粒子恰好不能从第n层磁场右侧边界穿出,试问在其他条件不变的情况下,也进入第n层磁场,但比荷较该粒子大的粒子能否穿出该层磁场右侧边界,请简要推理说明之。
如图所示,凸字形硬质金属线框质量为
,相邻各边互相垂直,且处于同一竖直平面内,
边长为
,
边长为
,
与
平行,间距为
。匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面。开始时,
边到磁场上边界的距离为
,线框由静止释放,从
边进入磁场直到
、
边进入磁场前,线框做匀速运动,在
、
边离开磁场后,
边离开磁场之前,线框又做匀速运动。线框完全穿过磁场过程中产生的热量为
。线框在下落过程中始终处于原竖直平面内,且
.
边保持水平,重力加速度为
;求 
(1)线框
边将离开磁场时做匀速运动的速度大小是
边刚进入磁场时的几倍
(2)磁场上下边界间的距离
如图所示,金属导轨
和
,
与
平行且间距为
,所在平面与水平面夹角为
,
、
连线与
垂直,
、
间接有阻值为R的电阻;光滑直导轨
和
在同一水平面内,与
的夹角都为锐角
。均匀金属棒
和
质量均为
,长均为
,
棒初始位置在水平导轨上与
重合;
棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为
(
较小),由导轨上的小立柱1和2阻挡而静止。空间有方向竖直的匀强磁场(图中未画出)。两金属棒与导轨保持良好接触。不计所有导轨和
棒的电阻,
棒的阻值为
,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为
。 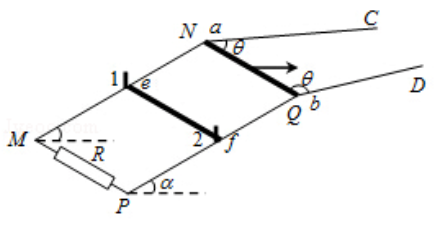
(1)若磁感应强度大小为B,给 棒一个垂直于 、水平向右的速度 ,在水平导轨上沿运动方向滑行一段距离后停止, 棒始终静止,求此过程 棒上产生的热量;
(2)在(1)问过程中, 棒滑行距离为 ,求通过 棒某横截面的电荷量;
(3)若 棒以垂直于 的速度 在水平导轨上向右匀速运动,并在 位置时取走小立柱1和2,且运动过程中 棒始终静止。求此状态下最强磁场的磁感应强度及此磁场下 棒运动的最大距离。
如图所示,粗糙、绝缘的直轨道
固定在水平桌面上,
端与桌面边缘对齐,
是轨道上一点,过
点并垂直于轨道的竖直面右侧有大小
,方向水平向右的匀强电场。带负电的小物体
电荷量是
,质量
,与轨道间动摩擦因数
,
从
点由静止开始向右运动,经过
到达
点,到达
点时速度是
,到达空间
点时速度与竖直方向的夹角为
,且
。
在整个运动过程中始终受到水平向右的某外力
作用,
大小与
的速率
的关系如表所示。
视为质点,电荷量保持不变,忽略空气阻力,取
,求:
(1)小物体
从开始运动至速率为
所用的时间;
(2)小物体
从
运动至
的过程,电场力做的功。
严重的雾霾天气,对国计民生已造成了严重的影响,汽车尾气是形成雾霾的重要污染源,"铁腕治污"已成为国家的工作重点,地铁列车可实现零排放,大力发展地铁,可以大大减少燃油公交车的使用,减少汽车尾气排放。若一地铁列车从甲站由静止启动后做直线运动,先匀加速运动20s达到最高速度72 / ,再匀速运动80 ,接着匀减速运动15 到达乙站停住。设列车在匀加速运动阶段牵引力为1×106 ,匀速阶段牵引力的功率为6×103 ,忽略匀减速运动阶段牵引力所做的功。

(1)求甲站到乙站的距离;
(2)如果燃油公交车运行中做的功与该列车从甲站到乙站牵引力做的功相同,求公交车排放气体污染物的质量。(燃油公交车每做1焦耳功排放气体污染物3×10-6克)