(12分)如图,直角三角形ABC的顶点坐标A( )、B(0,
)、B(0, ),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究
),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究 是否是定值?若是,求出定值;若不是,请说明理由.
是否是定值?若是,求出定值;若不是,请说明理由.
若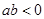 且
且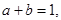 二项式
二项式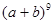 按
按 的降幂排列,展开后其第二项不大于第三项,求
的降幂排列,展开后其第二项不大于第三项,求 的取值范围。
的取值范围。
已知函数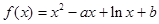
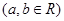 ,
,
(1)若函数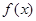 在
在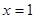 处的切线方程为
处的切线方程为 ,求实数
,求实数 的值;
的值;
(2)若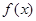 在其定义域内单调递增,求
在其定义域内单调递增,求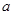 的取值范围.
的取值范围.
已知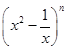 展开式中的二项式系数的和比
展开式中的二项式系数的和比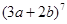 展开式的二项式系数的和大
展开式的二项式系数的和大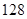 ,求
,求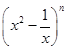 展开式中的系数最大的项和系数最小的项.
展开式中的系数最大的项和系数最小的项.
现有9本不同的书,分别求下列情况的不同分法的种数。
(1)分成三组,一组4本,一组3本,一组2本;
(2)分给三人,一人4本,一人3本,一人2本;
(3)平均分成三组。
设函数f(x)=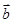 ×
×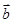 ,其中向量
,其中向量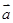 ="(2cosx,1),"
="(2cosx,1)," 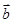 =(cosx,
=(cosx,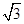 sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间;
(2)当xÎ[0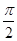 ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围.