如图所示，物块C质量mc=4kg，上表面光滑，左边有一立柱，放在光滑水平地面上。一轻弹簧左端与立柱连接，右端与物块B连接，mB=2kg；竖直放置的半径R=1.8m的光滑四分之一圆弧最低点的切线水平，且与物块C上表面在同一水平面上。物块A从圆弧的顶点静止释放，达到最低点时炸裂成质量m1=2kg，m2=1kg的两个物块1和2，物块1水平向左运动与B粘合在一起，物块2具有水平向右的速度，刚好回到圆弧的最高点。A、B都可以看着质点。取g="10" m/s2。求：
(1) 物块A炸裂时增加的机械能△E是多少？
(2) 在以后的过程中，弹簧最大的弹性势能Epm是多大？
在空间中存在垂直纸面向里的匀强磁场，其竖直边界AB.CD的宽度为d，在边界AB左侧是竖直向下、场强为E的匀强电场，现有质量为m、带电量为+q的粒子（不计重力）从P点以大小为
的水平初速度射入电场，随后与边界AB成45°射入磁场，若粒子能垂直CD边界飞出磁场，穿过小孔进入如图所示两竖直平行金属板间的匀强电场中减速至零且不碰到正极板。
（1）求出粒子进入磁场时的速度大小；
（2）求匀强磁场的磁感应强度B；
（3）求金属板间的电压U的最小值。
如图甲所示，电荷量为q=
C的带正电的小物块置于绝缘水平面上，所在空间存在方向沿水平向右的电场，电场强度E的大小与时间的关键如图乙所示，物块运动速度与时间t的关系如图丙所示，取重力加速度
，求：
（1）前2s内电场力做的功；
（2）物块的质量；
（3）物块与水平面的动摩擦因数。
如图，质量分别为m1=1.0kg和m2=2.0kg的弹性小球a、b，用弹性轻绳紧紧的把它们捆在一起，使它们发生微小的形变。该系统以速度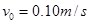
沿光滑水平面向右做直线运动，某时刻轻绳突然自动断开，断开后两球仍沿原直线运动，经过时间t=5.0s后，测得两球相距s=4.5m，求：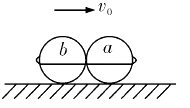
①刚分离时a、b两小球的速度大小v1、v2；
②两球分开过程中释放的弹性势能Ep。
如图所示，横截面为直角三角形的玻璃砖ABC，AC边长为L，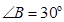
，光线P、Q同时由AC中点射入玻璃砖，其中光线P方向垂直AC边，光线Q方向与AC边夹角为
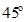，发现光线Q第一次到达BC边后垂直BC边射出，光速为c，求：
①玻璃砖的折射率；
②光线P由进入玻璃砖到第一次由BC边出射经历的时间
如图所示，内壁光滑的气缸竖直放置，在距气缸底部l=36cm处有一与气缸固定连接的卡环，活塞与气缸底部之间封闭了一定质量的气体。当气体的温度T1=300K、大气压强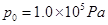
时，活塞与气缸底部之间的距离
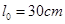，已知活塞面积为
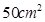，不计活塞的质量和厚度，现对缸内气体加热，使活塞缓慢上升当温度上升至
时，求：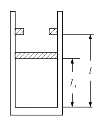
①封闭气体此时的压强；
②该过程中气体对外做的功；