(本题满分14分) 设数列
设数列 的前
的前 项和为
项和为 ,且
,且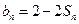 ;数列
;数列 为等差数列,且
为等差数列,且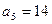 ,
, .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 若 ,
, 为数列
为数列 的前
的前 项和. 求证:
项和. 求证: .
.
(本小题满分12分)
已知向量 ,且与向量
,且与向量 的夹角为
的夹角为 ,其中
,其中 是
是 的内角
的内角
(1)求角 的大小
的大小
(2)求 的取值范围
的取值范围
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
(本小题满分12分)
已知函数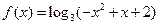 的定义域为集合
的定义域为集合 ,
, 的值域为集合
的值域为集合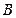 ,
, .(1)求
.(1)求 和
和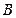 ; (2)求
; (2)求 、
、 .
.
设 是给定的正整数,有序数组
是给定的正整数,有序数组 同时满足下列条件:
同时满足下列条件:
①  ,
, ; ②对任意的
; ②对任意的 ,都有
,都有 .
.
(1)记 为满足“对任意的
为满足“对任意的 ,都有
,都有 ”的有序数组
”的有序数组 的个数,求
的个数,求 ;
;
(2)记 为满足“存在
为满足“存在 ,使得
,使得 ”的有序数组
”的有序数组 的个数,求
的个数,求
如图,正四棱柱 中,设
中,设 ,
, ,
,
若棱 上存在点
上存在点 满足
满足
 平面
平面 ,求实数
,求实数 的取值范围
的取值范围