(本题满分12分)
函数f(x)=x3+bx2+cx+d图象经过点(0,2),且在x=-1处的切线方程为6x - y+7=0.
(1)求函数f(x)解析式;
(2)求函数 f(x)的单调递减区间;
(3)求函数f(x)在[0,2]上的最大值和最小值.
有一批运动服装原价为每套80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一套减4元,买两套每套减8元,买三套每套减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一套运动服装,问选择哪个商场购买更省钱?
已知函数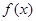
 的图像与
的图像与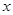 轴有两个交点
轴有两个交点
(1)设两个交点的横坐标分别为 试判断函数
试判断函数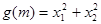 有没有最大值或最小值,并说明理由.
有没有最大值或最小值,并说明理由.
(2)若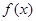
 与
与 在区间
在区间 上都是减函数,求实数
上都是减函数,求实数 的取值范围.
的取值范围.
设函数 ,
,
(1)作出 的图像;
的图像;
(2)求满足 的
的 的取值.
的取值.
设集合 ,
,
 ,
,
(1)当 时,求
时,求 与
与 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分11分)已知函数 .
.
(Ⅰ)求函数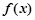 的单调递增区间;
的单调递增区间;
(Ⅱ)若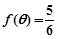 ,
,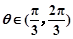 ,求
,求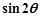 的值.
的值.