已知数列
 中,
中, ,
, 且
且 ,其前
,其前 项和为
项和为 ,且当
,且当 时,
时, .
.
⑴求证:数列 是等比数列;
是等比数列;
⑵求数列 的通项公式;
的通项公式;
⑶若 ,令
,令 ,记数列
,记数列 的前
的前 项和为
项和为 .设
.设
 是整数,问是否存在正整数
是整数,问是否存在正整数 ,使等式
,使等式 成立?若存在,求出
成立?若存在,求出 和相应的
和相应的 值;若不存在,请说明理由.
值;若不存在,请说明理由.
已知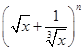 的展开式的二项式系数之和比(a+b)2n的展开式的系数之和小240,求
的展开式的二项式系数之和比(a+b)2n的展开式的系数之和小240,求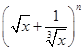 n的展开式中系数最大的项.
n的展开式中系数最大的项.
求证:1+2+22+…+25n-1能被31整除.
为拉动经济增长,某市决定新建一批基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目个数分别占总数的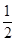 ,
,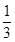 ,
,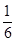 ,现在3名工人独立地从中任意一个项目参与建设.
,现在3名工人独立地从中任意一个项目参与建设.
(1)求他们选择的项目所属类别互不相同的概率.
(2)记X为3人中选择的项目所属于基础设施工程或产业建设工程的人数,求X的分布列及数学期望.
形状如图所示的三个游戏盘中(图①是正方形,M,N分别是所在边中点,图②是半径分别为2和4的两个同心圆,O为圆心,图③是正六边形,点P为其中心)各有一个玻璃小球,依次摇动三个游戏盘后,将它们水平放置,就完成了一局游戏.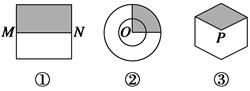
(1)一局游戏后,这三个盘中的小球都停在阴影部分的概率是多少?
(2)用随机变量X表示一局游戏后,小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值,求随机变量X的分布列.
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱)
(1)求在一次游戏中
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).