(满分12分)
某大学毕业生参加某单位的应聘考试,考核依次分为笔试,面试、实际操作共三轮进行,规定只有通过前一轮考核才能进入下一轮考核,否则被淘汰,三轮考核都通过才能被正式录用,设该大学毕业生通过一、二、三轮考核的概率分别为 ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。
①求该大学毕业生进入第三轮考核的概率;
②设该大学毕业生在应聘考核中考核轮数为X,求X的概率分布列及期望和方差。
选修4—1:几何证明选讲.
已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.
(Ⅰ)求∠BAE 的度数;
(Ⅱ)求证:
设函数
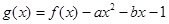 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)已知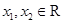 ,求证:
,求证: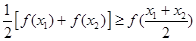 ;
;
(Ⅱ)函数 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值.
设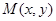 到定点
到定点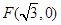 的距离和它到直线
的距离和它到直线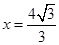 距离的比是
距离的比是 .
.
(Ⅰ)求点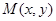 的轨迹方程;
的轨迹方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为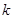 的直线过
的直线过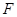 点,且与点
点,且与点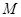 的轨迹交于点
的轨迹交于点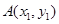 ,
,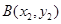 ,若
,若 ,求△
,求△ 的面积.
的面积.
在梯形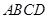 中,
中, ,
, ,
, ,
, ,如图把
,如图把 沿
沿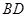 翻折,使得平面
翻折,使得平面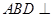 平面
平面 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若点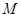 为线段
为线段 中点,求点
中点,求点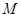 到平面
到平面 的距离.
的距离.
某市为了了解“陕西分类招生考试”宣传情况,从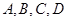 四所中学的学生当中随机抽取50名学生参加问卷调查,已知
四所中学的学生当中随机抽取50名学生参加问卷调查,已知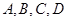 四所中学各抽取的学生人数分别为15,20,10,5.
四所中学各抽取的学生人数分别为15,20,10,5.
(Ⅰ)从参加问卷调查的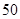 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
(Ⅱ)在参加问卷调查的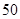 名学生中,从来自
名学生中,从来自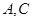 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用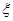 表示抽得
表示抽得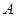 中学的学生人数,求
中学的学生人数,求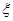 的分布列及期望值.
的分布列及期望值.