已知函数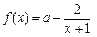 .
.
(1)当a = 4,解不等式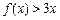 ;
;
(2)若函数 是奇函数,求a的值;
是奇函数,求a的值;
(3)若不等式 在
在 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
选修4-5:不等式选讲(本小题满分10分)
已知函数 ,若关于x的不等式
,若关于x的不等式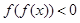 的解集为空集,求实数a的取值范围.
的解集为空集,求实数a的取值范围.
选修4-2:矩阵与变换(本小题满分10分)
已知矩阵 ,向量
,向量 ,求向量
,求向量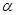 ,使得
,使得 .
.
选修4-1:几何证明选讲(本小题满分10分)
如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E. 若EB=6,EC=6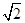 ,求BC的长.
,求BC的长.
(本小题满分16分) 对于项数为 的有穷数列
的有穷数列 ,记
,记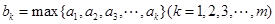 ,即
,即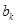 为
为 中的最大值,则称
中的最大值,则称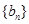 是
是 的“控制数列”,
的“控制数列”,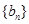 各项中不同数值的个数称为
各项中不同数值的个数称为 的“控制阶数”.
的“控制阶数”.
(Ⅰ)若各项均为正整数的数列 的控制数列
的控制数列 为
为 ,写出所有的
,写出所有的 ;
;
(Ⅱ)若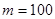 ,
, ,其中
,其中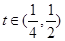 ,
,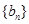 是
是 的控制数列,试用
的控制数列,试用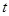 表示
表示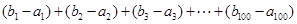 的值;
的值;
(Ⅲ)在 的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
(本小题满分16分)已知函数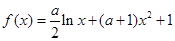 .
.
(Ⅰ)当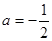 时,求
时,求 在区间
在区间 上的最小值;
上的最小值;
(Ⅱ)讨论函数 的单调性;
的单调性;
(Ⅲ)当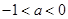 时,有
时,有 恒成立,求
恒成立,求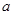 的取值范围.
的取值范围.