为了迎接2010年在广州举办的亚运会,我市某体校计划举办一次宣传活动,届时将在运动场的一块空地ABCD(如图)上摆放花坛,已知运动场的园林处(P点)有一批鲜花,今要把这批鲜花沿道路PA或PB送到空地ABCD中去,且PA="200" m,PB="300" m,∠APB=60°.
(1)试求A、B两点间的距离;
(2)能否在空地ABCD中确定一条界线,使位于界线一侧的点,沿道路PA送花较近;而另一侧的点,沿道路PB送花较近?如果能,请说出这条界线是一条什么曲线,并求出其方程.
抛物线 的准线与
的准线与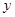 轴交于
轴交于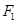 ,焦点为
,焦点为 ,若椭圆
,若椭圆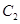 以
以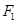 、
、 为焦点、且离心率为
为焦点、且离心率为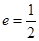 .
.
(1)当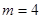 时,求椭圆
时,求椭圆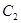 的方程;
的方程;
(2)若抛物线 与直线
与直线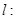
 及
及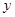 轴所围成的图形的面积为
轴所围成的图形的面积为 ,求抛物线
,求抛物线 和直线
和直线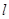 的方程.
的方程.
某单位为了提高员工素质,举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如图所示的茎叶图(单位:分),分数在175分以上(含175分)者定为“运动健将”,并给予特别奖励,其他人员则给予“运动积极分子”称号.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人,然后再从这10人中选4人,求至少有1人是“运动健将”的概率;
(2)若从所有“运动健将”中选3名代表,求所选代表中女“运动健将”恰有2人的概率.
如图所示,在四棱锥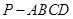 中,底面
中,底面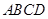 为矩
为矩
形,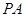 ⊥平面
⊥平面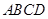 ,
, ,
,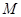 为
为 上的点,若
上的点,若 ⊥平面
⊥平面
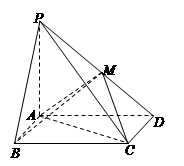
(1)求证: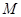 为
为 的中点;
的中点;
(2)求二面角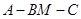 的大小.
的大小.
设函数 .
.
(1)求f(x)的单调区间;
(2)若当x∈[-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围.
在△ABC中,角A,B,C的对边分别为a,b,c,cos  =
= .
.
(1)求cosB的值;
(2)若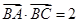 ,b=2
,b=2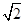 ,求a和c的值.
,求a和c的值.