(本小题满分12分)
已知铁矿石 和
和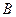 的含铁率为
的含铁率为 ,冶炼每万吨铁矿石的
,冶炼每万吨铁矿石的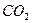 的排放量
的排放量 及每万吨铁矿石的价格
及每万吨铁矿石的价格 如下表:
如下表:
| |
 |
 (万吨) (万吨) |
 (百万元) (百万元) |
 |
50% |
1 |
3 |
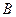 |
70% |
0.5 |
6 |
某冶炼厂计划至少生产1.9万吨铁,若要求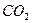 的排放量不超过
的排放量不超过 万吨,求所需费用的最小值,并求此时铁矿石
万吨,求所需费用的最小值,并求此时铁矿石 或
或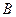 分别购买多少万吨.
分别购买多少万吨.
已知函数 在
在 上为增函数,且
上为增函数,且 ,
, 为常数,
为常数, .
.
(1)求 的值;
的值;
(2)若 在
在
 上为单调函数,求
上为单调函数,求 的取值范围;
的取值范围;
(3)设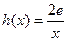 ,若在
,若在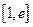 上至少存在一个
上至少存在一个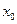 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
已知椭圆C的中心在原点,焦点在 轴上,椭圆上的点到左、右焦点
轴上,椭圆上的点到左、右焦点 的距离之和为
的距离之和为 ,离心率
,离心率 .
.
(1)求椭圆C的方程;
(2)过左焦点 的直线
的直线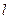 与椭圆C交于点
与椭圆C交于点 ,以
,以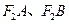 为邻边作平行四边形
为邻边作平行四边形 ,求该平行四边形对角线
,求该平行四边形对角线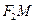 的长度的取值范围.
的长度的取值范围.
如图:在直角三角形ABC中,已知 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角 的大小记为
的大小记为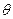 .
.
⑴求证:平面 平面BCD;
平面BCD;
⑵当 时,求
时,求 的值;
的值;
⑶在⑵的条件下,求点C到平面 的距离.
的距离.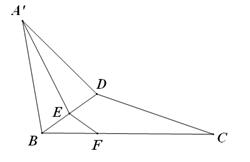
已知数列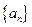 中,
中,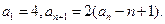
(1)求证:数列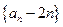 为等比数列;
为等比数列;
(2)设数列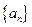 的前
的前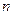 项的和为
项的和为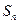 ,若
,若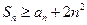 ,求:正
,求:正 整数
整数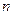 的最小值.
的最小值.
向量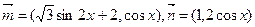 ,设函数
,设函数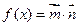 .
.
(1)求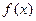 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在 中,
中,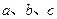 分别是角
分别是角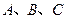 的对边,若
的对边,若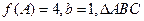 的面积为
的面积为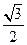 ,求
,求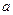 的值.
的值.