在各项均为正数的数列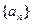 中,前
中,前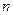 项和
项和 满足
满足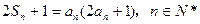 。
。
(1)证明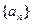 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前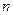 项和的公式;
项和的公式;
(2)在平面直角坐标系 面上,设点
面上,设点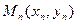 满足
满足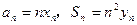 ,且点
,且点 在直线
在直线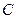 上,
上, 中最高点为
中最高点为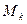 ,若称直线
,若称直线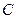 与
与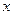 轴、直线
轴、直线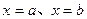 所围成的图形的面积为直线
所围成的图形的面积为直线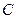 在区间
在区间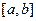 上的面积,试求直线
上的面积,试求直线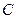 在区间
在区间 上的面积;
上的面积;
(3)求出圆心在直线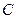 上的圆,使得点列
上的圆,使得点列 中任何一个点都在该圆内部
中任何一个点都在该圆内部
已知椭圆C: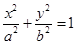 (
(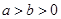 )的短轴长为2,离心率为
)的短轴长为2,离心率为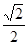 .
.
(1)求椭圆C的方程
(2)若过点M(2,0)的引斜率为 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足 (O为坐标原点),当
(O为坐标原点),当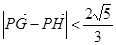 时,求实数
时,求实数 的取值范围?
的取值范围?
·大纲理)已知双曲线C: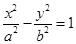 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、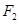 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为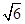 .
.
(1)求a,b;
(2)设过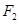 的直线l与C的左、右两支分别交于A、B两点,且
的直线l与C的左、右两支分别交于A、B两点,且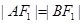 ,证明:
,证明: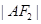 、
、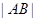 、
、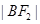 成等比数列.
成等比数列.
已知椭圆 的离心率为
的离心率为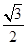 ,且经过点
,且经过点 ,圆
,圆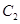 的直径为
的直径为 的长轴.如图,
的长轴.如图,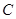 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线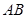 过点
过点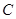 且与圆
且与圆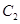 交于
交于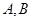 两点,
两点,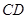 垂直于
垂直于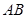 交椭圆于点
交椭圆于点 .
.
(1)求椭圆 的方程;
的方程;
(2)求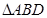 面积的最大值,并求此时直线
面积的最大值,并求此时直线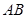 的方程.
的方程.
已知点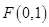 直线
直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 作直线
作直线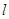 的垂线,垂足为
的垂线,垂足为 ,且
,且 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)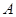 、
、 是轨迹
是轨迹 上异于坐标原点
上异于坐标原点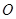 的不同两点,轨迹
的不同两点,轨迹 在点
在点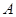 、
、 处的切线分别为
处的切线分别为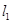 、
、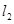 ,且
,且 ,
,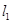 、
、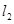 相交于点
相交于点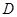 ,求点
,求点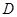 的纵坐标.
的纵坐标.
已知双曲线 的中心为原点
的中心为原点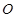 ,左、右焦点分别为
,左、右焦点分别为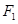 、
、 ,离心率为
,离心率为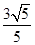 ,点
,点 是直线
是直线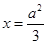 上任意一点,点
上任意一点,点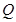 在双曲线
在双曲线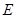 上,且满足
上,且满足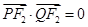 .
.
(1)求实数 的值;
的值;
(2)证明:直线 与直线
与直线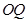 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为 ,过点
,过点 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、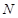 ,在线段
,在线段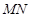 上去异于点
上去异于点 、
、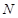 的点
的点 ,满足
,满足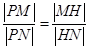 ,证明点
,证明点 恒在一条定直线上.
恒在一条定直线上.