(本小题满分12分)
2010年 上海世博会大力倡导绿色出行,并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量,某游客计划在游园期间种植n棵树,已知每棵树是否成活互不影响,成活率都为
上海世博会大力倡导绿色出行,并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量,某游客计划在游园期间种植n棵树,已知每棵树是否成活互不影响,成活率都为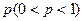 ,用
,用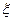 表示他所种植的树中成活的棵数,
表示他所种植的树中成活的棵数,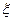 的数学期望为E
的数学期望为E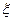 ,方差为D
,方差为D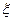 。
。
(I) 若n=1,求D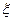 的最大值;
的最大值;
(II) 已知E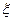 =3,标准差
=3,标准差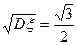 ,试求n与p的值并写出
,试求n与p的值并写出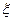 的分布列。
的分布列。
(本小题满分12分)已知函数
(I)求函数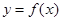 图象的对称轴方程;
图象的对称轴方程;
(II)求函数 的最小正周期和值域.
的最小正周期和值域.
(本小题满分10分)设函数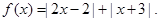
(I)解不等式 ;
;
(II)若关于x的不等式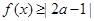 恒成立,试求a的取值范围.
恒成立,试求a的取值范围.
已知函数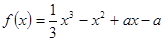 (
(
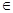 R).
R).
(1) 当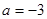 时,求函数
时,求函数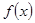 的极值;
的极值;
(2)若函数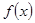 的图象与
的图象与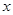 轴有且只有一个交点,求a的取值范围.
轴有且只有一个交点,求a的取值范围.
(本小题满分14分)
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
…… … …
…… … ……
假设第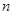 行的第二个数为
行的第二个数为 ,
,
(Ⅰ)依次写出第六行的所有 个数字;
个数字;
(Ⅱ)归纳出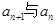 的关系式并求出
的关系式并求出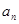 的通项公式;
的通项公式;
(Ⅲ)设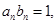 求证:
求证:
(本小题满分14分)
设椭圆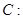
 的离心率为
的离心率为 =
=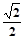 ,点
,点 是椭圆上的一点,
是椭圆上的一点,
且点 到椭圆
到椭圆 两焦点的距离之和为4.
两焦点的距离之和为4.
(1)求椭圆 的方程;
的方程;
(2)椭圆 上一动点
上一动点
 关于直线
关于直线 的对称点为
的对称点为 ,
,
求 的取值范围.
的取值范围.