(本题满分13 分)
已知椭圆的右焦点F 与抛物线y2 =" 4x" 的焦点重合,短轴长为2.椭圆的右准线l与x轴交于E,过右焦点F 的直线与椭圆相交于A、B 两点,点C 在右准线l上,BC//x 轴.
(1)求椭圆的标准方程,并指出其离心率;
(2)求证:线段EF被直线AC 平分.
【改编】(本小题满分12分)在数列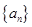 中,已知
中,已知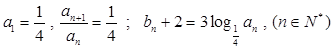
(Ⅰ)求数列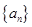 、
、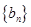 的通项公式;
的通项公式;
(Ⅱ)设数列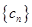 满足
满足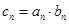 ,求
,求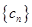 的前n项和
的前n项和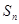 .
.
【改编】(本小题满分12分)已知三棱柱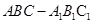 中,侧棱垂直于底面,
中,侧棱垂直于底面,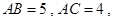
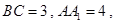 点
点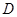 在
在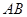 上.
上.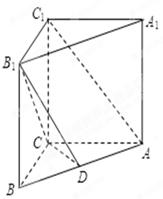
(Ⅰ)若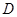 是
是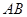 中点,求证:
中点,求证: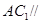 平面
平面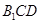 ;
;
(Ⅱ)当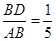 时,求三棱锥
时,求三棱锥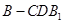 的体积.
的体积.
(本小题满分12分)为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如下: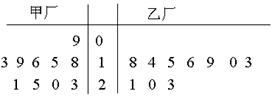
规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品.
(Ⅰ)试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小;
(Ⅱ)现从乙厂抽出的非优等品中随机抽取两件,求至少抽到一件该元素含量为10毫克或13毫克的产品的概率.
(本小题满分12分) 已知向量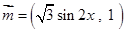 ,
, ,设函数
,设函数 .
.
(Ⅰ)求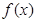 的单调递增区间;
的单调递增区间;
(Ⅱ)在△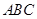 中,
中, 、
、 、
、 分别是角
分别是角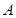 、
、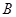 、
、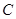 的对边,若
的对边,若 ,
,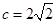 ,
,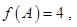 求
求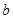 .
.
(本小题满分10分)对于给定的函数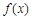 ,定义
,定义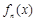 如下:
如下: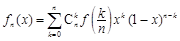 ,其中
,其中 .
.
(1)当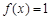 时,求证:
时,求证: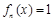 ;
;
(2)当 时,比较
时,比较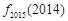 与
与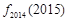 的大小;
的大小;
(3)当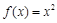 时,求
时,求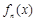 的不为0的零点.
的不为0的零点.