如图12所示，A为一具有光滑曲面的固定轨道，轨道底端是水平的，质量M=40kg的上车B静止于轨道右侧，其板面与轨道底端靠近且在同一水平面上，一个质量m="20" kg，可视为质点的小滑块C以
的初速度从轨道顶端滑下，C冲上小车B后，经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差为
，C与小车板面间的动摩擦因数为
，小车与水平面间的摩擦不计，
取10m/s2。求
（1）C与小车保持相对静止时的速度大小。
（2）从C冲上小车瞬间到与小车相对静止瞬间所用的时间。
（3）C冲上小车后相对于小车板面滑动的距离。
如图所示，直角三角形导线框ABC，处于磁感强度为B的匀强磁场中，线框在纸面上绕B点以匀角速度ω作顺时针方向转动，∠B=60°，∠C=90°，AB=l，求A，C两端的电压UAC。
用均匀导线弯成正方形闭合金属线框abcd，线框每边长80cm，每边的电阻为0.01Ω。把线框放在磁感强度B=0.05T的匀强磁场中，并使它绕轴OO′以ω=100rad/s的角速度匀角速度旋转，旋转方向如图所示。已知OO’在线框平面内，并且垂直于B，
，
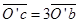，当线框转至和B平行的瞬间，求
（1）每条边产生的感应动势大小；
（2）线框内感应电流的大小；
（3）e，f分别是ab和cd的中点，ef两点间的电势差。
如图所示光滑平行金属轨道abcd，轨道的水平部分bcd处于竖直向上的匀强磁场中，bc部分平行导轨宽度是cd部分的2倍，轨道足够长。将质量相同的金属棒P和Q分别置于轨道的ab段和cd段。P棒位于距水平轨道高为h的地方，放开P棒，使其自由下滑，求P棒和Q棒的最终速度。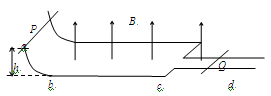
如图所示，长为6m的导体AB在磁感强度B=0.1T的匀强磁场中，以AB上的一点O为轴，沿着顺时针方向旋转。角速度ω=5rad/s，O点距A端为2m，求AB的电势差。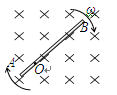
在如图所示的水平导轨上（摩擦、电阻忽略不计），有竖直向下的匀强磁场，磁感强度B，导轨左端的间距为L1=4l0，右端间距为l2=l0。今在导轨上放置AC、DE两根导体棒，质量分别为m1=2m0，m2=m0，电阻R1=4R0，R2=R0。若AC棒以初速度v0向右运动，求AC棒运动的过程中产生的总焦耳热QAC，以及通过它们的总电量q。