(本小题满分12分)如图,在四边形ABCD中,AC⊥BD,垂足为O,PO⊥平面ABCD,AO=BO=DO=1,CO=PO=2,E是线段PA上的点,AE∶AP=1∶3.
(1) 求证:OE∥平面PBC;
(2)求二面角D-P B-C的大小.
B-C的大小.
已知函数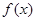
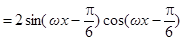 (其中
(其中 >0,
>0,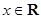 )的最小正周期为
)的最小正周期为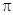 .
.
(1)求 的值;
的值;
(2)在△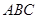 中,若A<B,且
中,若A<B,且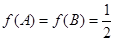 ,求
,求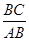
已知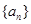 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且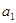 ,
,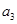 ,
, 成等比数列.
成等比数列.
(I)求数列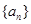 的通项;
的通项;
(II)记 ,数列
,数列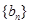 的前
的前 项和为
项和为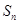 .求证
.求证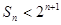
已知函数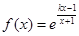 (e是自然对数的底数).
(e是自然对数的底数).
(1)若函数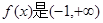 上的增函数,求
上的增函数,求 的取值范围;
的取值范围;
(2)若对任意的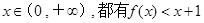 ,求满足条件的最大整数
,求满足条件的最大整数 的值.
的值.
已知 ,
,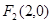 ,点
,点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为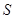 ,过点
,过点 作直线
作直线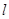 与轨迹
与轨迹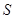 交于
交于 两点,过
两点,过 作直线
作直线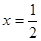 的垂线
的垂线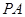 、
、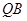 ,垂足分别为
,垂足分别为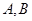 ,记
,记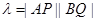 。
。
(1)求轨迹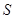 的方程;
的方程;
(2)设点 ,求证:当
,求证:当 取最小值时,
取最小值时, 的面积为
的面积为 .
.
已知数列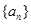 是各项均不为0的等差数列,
是各项均不为0的等差数列,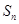 为其前n项和,且满足
为其前n项和,且满足 ,数列
,数列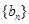 满足
满足 为数列
为数列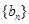 的前n项和。
的前n项和。
(1)求数列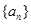 的通项
的通项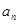 和
和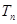 ;
;
(2)若对任意的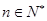 ,不等式
,不等式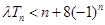 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。