(本小题满分14分)

|


 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
|

 所成的角为45°,底面ABCD为直角梯形,
所成的角为45°,底面ABCD为直角梯形,
|



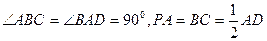
|
|
 (Ⅰ)求证:平面
(Ⅰ)求证:平面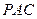 ⊥平面
⊥平面 ;
;
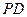 上是否存在一点
上是否存在一点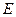 ,使
,使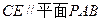 ?若存在,请确定E点的位置;若不存在,请说明理由.
?若存在,请确定E点的位置;若不存在,请说明理由..(本小题满分14分)
已知 。
。
(1)证明: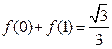
(2)分别求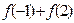 ,
, ;
;
(3)试根据(1)(2)的结果归纳猜想一般性结论,并证明你的结论.
(本小题满分14分)
如图, 在长方体 中,过
中,过 作
作 的垂线,垂足为
的垂线,垂足为 ,过
,过 作
作 的垂线,垂足为
的垂线,垂足为 。
。
(1)求证:
(2)判断 是否平行于平面
是否平行于平面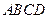 ,并证明你的结论
,并证明你的结论
(本小题满分14分)
抛物线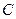 的顶点在原点,焦点F与双曲线
的顶点在原点,焦点F与双曲线 的右焦点重合,过点
的右焦点重合,过点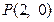 且斜率为1的直线
且斜率为1的直线 与抛物线
与抛物线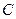 交于
交于 两点
两点
(1)求抛物线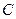 的方程
的方程
(2)求弦 中点到抛物线准线的距离
中点到抛物线准线的距离
(本小题满分12分)
设函数
(1)求 的表达式;
的表达式;
(2)若 ,求函数
,求函数 的单调区间、极大值和极小值
的单调区间、极大值和极小值
(本小题满分12分)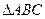 的内角
的内角 所对边长分别为
所对边长分别为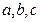 ,已知
,已知 ,
,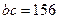
(1)求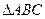 的面积
的面积
(2)若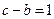 ,求
,求 的值
的值