如图,在直三棱柱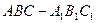 中,
中, ,点
,点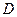 是
是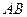 的中点,
的中点,
(1)求证: 平面
平面
(2)求证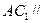 平面
平面
 |
有3本不同的语文书和3本不同的数学书,求满足下列条件的方法总数(用数字作答)
(1)6本排成一排;
(2)6本排成一排,其中3本数学书必须相邻;
(3)6本排成一排,其中语文书互不相邻.
在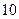 件产品中,有
件产品中,有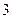 件一等品,
件一等品,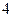 件二等品,
件二等品,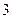 件三等品,从这
件三等品,从这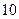 件产品中任取
件产品中任取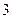 件
件
求:(1)取出的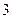 件产品中一等品的件数
件产品中一等品的件数 的分布列和数学期望
的分布列和数学期望
(2)取出的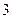 件产品中一等品的件数多余二等品件数的概率
件产品中一等品的件数多余二等品件数的概率
已知函数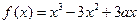
 在
在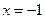 处,取得极值
处,取得极值
(1) 求实数 的值 (2) 求函数
的值 (2) 求函数 的单调区间,并指出其单调性。
的单调区间,并指出其单调性。
证明(1)已知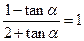 ,求证
,求证
(2)已知数列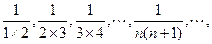 计算
计算 由此推算
由此推算 的公式,并用数学归纳法给出证明。
的公式,并用数学归纳法给出证明。