(10 分)地球质量为M、半径为R,万有引力常量为G,发射一颗绕地球表面附近做圆周运动的人造卫星,卫星的速度称为第一宇宙速度.
(1)试推导由上述各量表达的第一宇宙速度的计算式;
(2)若已知第一宇宙速度的大小v="7.9" km/s,地球半径R=6.4×103 km,万有引力常量G=6.7×10-11 N·m2/kg2,求地球质量(结果保留两位有效数字).
分如图(a)所示,质量为M = 10kg的滑块放在水平地面上,滑块上固定一个轻细杆ABC,∠ABC = 45°.在A端固定一个质量为m = 2kg的小球,滑块与地面间的动摩擦因数为m = 0.5.现对滑块施加一个水平向右的推力F1 = 84N,使滑块做匀加速运动.求此时轻杆对小球作用力F2的大小和方向.(取g=10m/s2)
有位同学是这样解的:
解:小球受到重力及杆的作用力F2,因为是轻杆,所以F2方向沿杆向上,受力情况如图(b)所示.根据所画的平行四边形,可以求得:
F2 =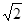 mg =
mg = 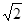 ×2×10N = 20
×2×10N = 20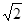 N.
N.
你认为上述解法是否正确?如果不正确,请说明理由,并给出正确的解答.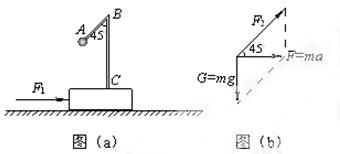
分2012年11月,我国舰载机在航母上首降成功。设某一载舰机质量为m = 2.5×104 kg,速度为v0=42m/s,若仅受空气阻力和甲板阻力作用,飞机将在甲板上以a0=0.8m/s2的加速度做匀减速运动,着舰过程中航母静止不动。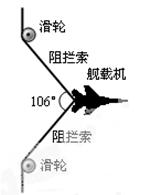
(1)飞机着舰后,若仅受空气阻力和甲板阻力作用,航母甲板至少多长才能保证飞机不滑到海里?
(2)空气阻力和甲板阻力
(3)为了让飞机在有限长度的跑道上停下来,甲板上设置了阻拦索让飞机减速,同时考虑到飞机尾钩挂索失败需要复飞的情况,飞机着舰时并不关闭发动机。图示为飞机勾住阻拦索后某一时刻的情景,此时发动机的推力大小为F = 1.2×105 N,减速的加速度a1=20m/s2,此时阻拦索夹角θ=106°,空气阻力和甲板阻力保持不变,求此时阻拦索承受的张力大小?
某运动员做跳伞训练,他从悬停在空中的直升飞机上由静止跳下,跳离飞机一段时间后打开降落伞做减速下落。他打开降落伞后的速度图线如图a。降落伞用8根对称的绳悬挂运动员,每根绳与中轴线的夹角均为37°,如图b。已知人的质量为50kg,降落伞质量也为50kg,不计人所受的阻力,打开伞后伞所受阻力f与速度v成正比,即f="kv" (g取10m/s2,sin53°=0.8,cos53°="0.6)" .求: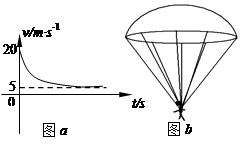
(1)打开降落伞前人下落的距离为多大?
(2)求阻力系数k和打开伞瞬间的加速度a的大小和方向?
(3)悬绳能够承受的拉力至少为多少?
如图所示,将质量m=0.1kg的圆环套在固定的水平直杆上。环的直径略大于杆的截面直径。环与杆间动摩擦因数m=0.8。对环施加一位于竖直平面内斜向上,与杆夹角q=53°的拉力F,使圆环以a=4.4m/s2的加速度沿杆运动,求F的大小。(取sin53°=0.8,cos53°=0.6,g=10m/s2)。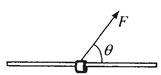
如图所示,在两条平行的虚线间存在着宽度为L、电场强度为E的匀强电场,在与右侧虚线相距为L处有一个与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求:
(1)粒子从射入到打到屏上所用的时间;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值;
(3)粒子打在屏上的点P到O距离y.