(本小题满分14分)
已知函数 .
.
(I)当 时,求曲线
时,求曲线 在点
在点 处切线的斜率;
处切线的斜率;
(II)当 时,求函数
时,求函数 的单调区间.
的单调区间.
设 是以
是以 为焦点的抛物线
为焦点的抛物线 ,
, 是以直线
是以直线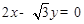 与
与 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.
(1)求双曲线 的标准方程;
的标准方程;
(2)若 与
与 在第一象限内有两个公共点
在第一象限内有两个公共点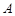 和
和 ,求
,求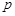 的取值范围,并求
的取值范围,并求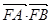 的最大值;(3)若
的最大值;(3)若 的面积
的面积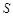 满足
满足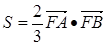 ,求
,求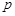 的值.
的值.
(理)设数列 为正项数列,其前
为正项数列,其前 项和为
项和为 ,且有
,且有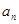 ,
, ,
, 成等差数列.(1)求通项
成等差数列.(1)求通项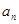 ;(2)设
;(2)设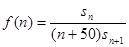 求
求 的最大值.
的最大值.
(文)数列 满足
满足
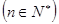 ,且
,且 .(1)求通项
.(1)求通项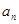 ;(2)记
;(2)记 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 .
.
如图所示,在长方体 中,
中, ,
, ,
, ,
, 为棱
为棱 上一点.
上一点.
(1)若 ,求异面直线
,求异面直线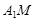 和
和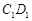 所成角的正切值;
所成角的正切值;
(2)是否存在这样的点 使得
使得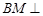 平面
平面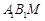 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(理)红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 的分布列和数学期望
的分布列和数学期望 .
.
已知向量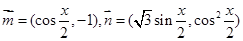 ,设函数
,设函数 +
+
(1)若 ,f(x)=
,f(x)=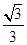 ,求
,求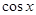 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是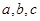 ,且满足
,且满足 ,求f(B)的值.
,求f(B)的值.