(本题12分)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
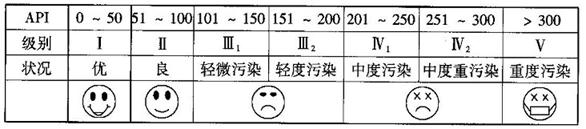
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间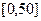 ,
,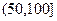 ,
,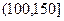 ,
, ,
,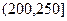 ,
,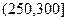 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量为良的天数;
(3)某环保部门准备在一年内随机到该城市考察两次空气质量,求两次考察空气质量都为良的概率(结果用分数表示).
(本小题满分12分)
如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分PC,且分别交AC、PC于D、E两 点,又PB=BC,PA=AB.
点,又PB=BC,PA=AB.
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)求线段PA上点Q的位置,使得PC//平面BDQ.
(本小题满分12分)
已知函数 .
.
(Ⅰ)若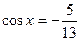 ,
, ,求函数
,求函数 的值;
的值;
( Ⅱ)将函数
Ⅱ)将函数 的图像向右平移
的图像向右平移 个单位,使平移后的
个单位,使平移后的 图像关于原点对称,若
图像关于原点对称,若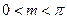 ,试求
,试求 的值.
的值.
(本小题满分12分)
青海玉树发生地震后,为重建,对某项工程进行竞标,现共有6家企业参与竞标,其中A企业来自辽宁省,B、C两家企业来自福建省,D、E、F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同。
(Ⅰ)列举所有企业的中标情况;
(Ⅱ)在中标的企业中,至少有一家来自福建省的概率是多少?
(本小题满分12分)已知等差数列 的前
的前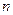 项和为
项和为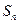 ,且
,且 ,
, .
.
(Ⅰ)求数列 的通项
的通项 ;
;
(Ⅱ)设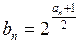 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分7分)选修4—5:不等式选讲
已知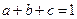 ,且
,且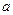 .
.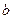 .
.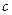 是正数,求证:
是正数,求证: .
.