(本小题满分12分)
如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分PC,且分别交AC、PC于D、E两 点,又PB=BC,PA=AB.
点,又PB=BC,PA=AB.
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)求线段PA上点Q的位置,使得PC//平面BDQ.
某市在进行城市环境建设中,要把一
个三角形的区域改造成市内公园. 经过测量得到这个
三角形区域的三条边长分别为
(不要求进行近似计算)
(1)求该三角形最大角的余弦值;
(2)求该三角形的面积. 
本题满分7分)已知关于 的不等式
的不等式
(1)当 时,解该不等式
时,解该不等式
(2)若不等式对一切实数 恒成立,求
恒成立,求 的取值范围.
的取值范围.
若S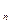 是公差不为0的等差数列
是公差不为0的等差数列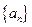 的前n项和,且
的前n项和,且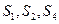 成等比数列。
成等比数列。
(1)求等比数列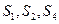 的公比; (2)若
的公比; (2)若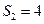 ,求
,求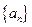 的通项公式;
的通项公式;
(3)设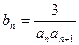 ,
,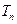 是数列
是数列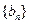 的前n项和,求使得
的前n项和,求使得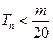 对所有
对所有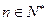 都成立的最小正整数m。
都成立的最小正整数m。
(共14分,每题各7分)
(1)已知集合 若
若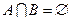 ,求实数
,求实数 的取值范围;
的取值范围;
(2)已知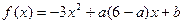 。当不等式
。当不等式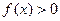 的解集为(-1,3)时,求实数
的解集为(-1,3)时,求实数 ,
,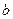 的值。
的值。
本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元。甲、乙电视台的广告收费标准分别为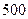 元/分钟和200元/分钟。假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元。问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟。假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元。问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?