(共14分,每题各7分)
(1)已知集合 若
若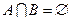 ,求实数
,求实数 的取值范围;
的取值范围;
(2)已知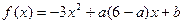 。当不等式
。当不等式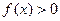 的解集为(-1,3)时,求实数
的解集为(-1,3)时,求实数 ,
,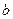 的值。
的值。
已知椭圆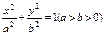 的离心率为
的离心率为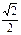 .
.
⑴若圆(x-2)2+(y-1)2=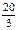 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
⑵设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600.求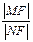 的值.
的值.
⑶在(1)的条件下,椭圆W的左右焦点分别为F1、 F2,点R在直线l:x-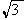 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求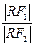 的值.
的值.
已知圆 过点
过点
 ,且与圆
,且与圆
 (
( >0)关于直线
>0)关于直线 对称,
对称,
⑴求圆 的方程;
的方程;
⑵过点 作两条直线分别与圆
作两条直线分别与圆 相交于点
相交于点 、
、 ,且直线
,且直线 和直线
和直线 的倾斜角互补,
的倾斜角互补, 为坐标原点,判断直线
为坐标原点,判断直线 与
与 是否平行,并请说明理由
是否平行,并请说明理由
如图,设有半径为3 的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
在△ABC中,BC固定,顶点A移动.设
 ,当三个角满足条件
,当三个角满足条件
 时,求A的轨迹方程
时,求A的轨迹方程
直线 过点
过点 ,倾斜角的正弦是
,倾斜角的正弦是 ,求直线
,求直线 的方程.
的方程.