(本题13分)已知函数
(1)已知一直线 经过原点
经过原点 且与曲线
且与曲线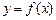 相切,求
相切,求 的直线方程;
的直线方程;
(2)若关于 的方程
的方程 有两个不等的实根,求实数
有两个不等的实根,求实数 的取值范围。
的取值范围。
(本小题满分12分)某地决定新建A,B,C三类工程,A,B,C三类工程所含项目的个数分别占总项目数的 (总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(Ⅰ)求他们选择的项目所属工程 类别相同的概率;
类别相同的概率;
(Ⅱ)记 为3人中选择的项目属于B类工程或C类工程的人数,求
为3人中选择的项目属于B类工程或C类工程的人数,求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)已知函数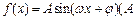 >0,
>0, >0,
>0, <
<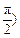 的图象与
的图象与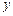 轴的交点为(0,1),它在
轴的交点为(0,1),它在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和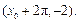
(1)写出 的解析式及
的解析式及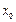 的值;(2)若锐角
的值;(2)若锐角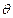 满足
满足 ,求
,求 的值.
的值.
 |
(本小题满分10分)选修4-5:不等式选讲已知对于任意非零实数 ,不等式
,不等式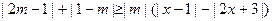 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题记分。
(本小题满分10分)选修4-1:几何证明选讲
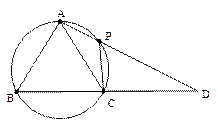
在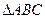 中,AB=AC,过点A的直线与其外接圆交
中,AB=AC,过点A的直线与其外接圆交
于点P,交BC延长线于点D。
(1)求证:  ;
;
(2)若AC=3,求 的值。
的值。
