质量为m="1" kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧的两端点,其连线水平.已知圆弧半径R="1.0" m,圆弧对应圆心角为θ=106°,轨道最低点为O,A点距水平面的高度h="0.8" m.小物块离开C点后恰能无碰撞的沿固定斜面向上运动,0.8 s后经过D点,物块与斜面间的滑动摩擦因数为μ=0.33(g="10" m/s2,sin37°=0.6,cos37°=0.8)试求: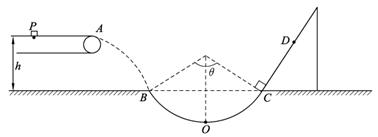
(1)小物块离开A点的水平初速度v1;
(2)小物块经过O点时对轨道的压力;
(3)斜面上CD间的距离
如图所示为一均匀薄壁U形管,左管上端封闭,右管开 口且足够长,管的横截面积为S,内装有密度为p的液体.右管 内有一质量为m的活塞搁在固定卡口上,卡口与左管上端等 高,活塞与管壁间无摩擦且不漏气.温度为T。时,左、右管内液 面等高,两管内空气柱(可视为理想气体)长度均为L,压强均 为大气压强P0,重力加速度为g,现使左、右两管温度同时缓慢 升高,在活塞离开卡口上升前,左右两管液面保持不动.求:
①温度升高到T1为多少时,右管活塞开始离开卡口上升;
②温度升高到T2为多少时,两管液面高度差为L.
如图甲所示,两根足够长的平行光滑金属导轨MN、PQ被固定在水平面上,导轨间距 l="0.6" m,两导轨的左端用导线连接电阻R1及理想电压表 ,电阻r=2Ω的金属棒垂直 于导轨静止在AB处;右端用导线连接电阻R2,已知R1=2Ω,R2=1Ω,导轨及导线电阻 均不计.在矩形区域CDEF内有竖直向上的磁场,CE="0.2" m,磁感应强度随时间的变化 如图乙所示.开始时电压表有示数,当电压表示数变为零后,对金属棒施加一水平向右 的恒力F,使金属棒刚进入磁场区域时电压表的示数又变为原来的值,金属棒在磁场运 动过程中电压表的示数始终保持不变.求:
,电阻r=2Ω的金属棒垂直 于导轨静止在AB处;右端用导线连接电阻R2,已知R1=2Ω,R2=1Ω,导轨及导线电阻 均不计.在矩形区域CDEF内有竖直向上的磁场,CE="0.2" m,磁感应强度随时间的变化 如图乙所示.开始时电压表有示数,当电压表示数变为零后,对金属棒施加一水平向右 的恒力F,使金属棒刚进入磁场区域时电压表的示数又变为原来的值,金属棒在磁场运 动过程中电压表的示数始终保持不变.求:
(1)t="0.1" s时电压表的读数;
(2)恒力F的大小;
(3)从t=0时刻到金属棒运动出磁场过程中整个电路产生的热量.
一氢气球的质量m="0.2" kg,在无风的天气,氢气球在轻绳的牵引下静止在空中, 此时轻绳的拉力F=10N.星期天,某儿童带氢气球到公园玩耍,休息时为了防止气球飞 掉,把轻绳系到一质量M="4" kg的木块上,如图所示,木块与水平地面间的动摩擦因数μ="0.3." 当有水平方向风吹来,气球受到水平风力F="kv(" k为一常数,v为风速),当风速v1="3" m/s时木块在地面上恰好静止.木块受到最大静摩 擦力等于滑动摩擦力,g="10" m/s2.求: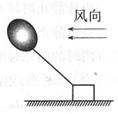
(1)气球受到的浮力;(2)若风速v2=6m/s,木块开始运动时的加速度大小.
如图,“蜗牛状”轨道OAB竖直固定,其最低点与平板车左端平滑对接,平板车静止在光滑水平面上。其中,“蜗牛状”轨道由内壁光滑的两个半圆轨道OA、AB平滑连接而成,轨道OA的半径R=0.6m,其下端O刚好是轨道AB的圆心。将一质量为m=0.5kg的小球从O点沿切线方向以某一初速度进入轨道OA后,可沿OAB轨道运动滑上平板车。取g=10m/s2. 
(1)若因受机械强度的限制,“蜗牛状”轨道AB段各处能承受最大挤压力为Fm=65N,则在保证轨道不受损情况下,该轨道最低点B处速度传感器显示速度范围如何?
(2)设平板车质量为M=2kg,平板车长度为L=2m,小球与平板车上表面动摩擦因数μ=0.5。现换用不同质量m的小球,以初速度v0= m/s从O点射入轨道,试讨论小球质量在不同取值范围内,系统因摩擦而相应产生的热量Q。
m/s从O点射入轨道,试讨论小球质量在不同取值范围内,系统因摩擦而相应产生的热量Q。
示波器的示波管中电子束是用电偏转技术实现的,电视机的显像管中电子束是用磁偏转技术实现的。图为磁场或电场实现电子束偏转的示意图,M为显示屏。已知灯丝正常工作,由灯丝发射出来的电子初速度可认为零,经加速电压为U1的电场加速,电子束从两极板正中央水平射入。已知电子质量为m、电荷量为q。当加一匀强磁场时能让电子束恰好射到极板的右下边缘,偏转角度最大为53°,已知极板长为4L,电子所受的重力大小忽略不计。(sin53°= 0.8,cos53°= 0.6),求:
(1)电子在该磁场中的偏转半径R和极板间距d分别为多少?
(2)此时所加的磁场的磁感强度B的值?
(3)若撤去磁场,改加竖直方向电场时也让电子束射到极板的右下边缘,则极板间的电压U2为多少?