如图所示，位于竖直平面内的光滑有轨道，由一段斜的直轨道与之相-优题课

如图所示，位于竖直平面内的光滑有轨道，由一段斜的直轨道与之相切的圆形轨道连接而成，圆形轨道的半径为 $R$ 。一质量为 $m$ 的小物块从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动。要求物块能通过圆形轨道最高点，且在该最高点与轨道间的压力不能超过5 $m g$ （ $g$ 为重力加速度）。求物块初始位置相对于圆形轨道底部的高度 $h$ 的取值范围。

科目物理题型解答题难度较难

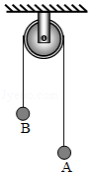
一细绳跨过悬挂的定滑轮，两端分别系有小球 $A$ 和 $B$ ，如图所示。一实验小组用此装置测量小球 $B$ 运动的加速度。令两小球静止，细绳拉紧，然后释放小球，测得小球 $B$ 释放时的高度 $h_{0} = 0.590 m$ ，下降一段距离后的高度 $h = 0.100 m$ ；由 $h_{0}$ 下降至 $h$ 所用的时间 $T = 0.730 s$ 。由此求得小球 $B$ 加速度的大小为 $a =$ 　　 $m / s^{2}$ （保留3位有效数字）。从实验室提供的数据得知，小球 $A$ 、 $B$ 的质量分别为 $100.0 g$ 和 $150.0 g$ ，当地重力加速度大小为 $g = 9.80 m / s^{2}$ ．根据牛顿第二定律计算可得小球 $B$ 加速度的大小为 $a' =$ 　　 $m / s^{2}$ （保留3位有效数字）。可以看出， $a'$ 与 $a$ 有明显差异，除实验中的偶然误差外，写出一条可能产生这一结果的原因：　　。

某游乐园入口旁有一喷泉, 喷出的水柱将一质量为 $M$ 的卡通玩具稳定地悬停在空中。为计算方便起见，假设水柱从横截面积为 $S$ 的喷口持续以速度 v0 竖直向上喷出; 玩具底部为平板（面积略大于 $S$ ); 水柱冲击到玩具底板后, 在竖直方向水的速度变为零, 在水平方向朝四周均匀散开。忽略空气阻力。已知水的密度为 $ρ$ , 重力加速度大小为 $g 。$ 求

(i) 喷泉单位时间内喷出的水的质量;

（ii）玩具在空中悬停时, 其底面相对于喷口的高度。

[物理——选修 3-3]

在水下气泡内空气的压强大于气泡表面外侧水的压强, 两压强差 $Δ p$ 与气泡半径

$r$ 之间的关系为 $Δ p = \frac{2 σ}{r}$ , 其中 $σ = 0.070 N / m$ 。现让水下 $10 m$ 处一半径为 $0.50 cm$ 的气泡缓慢上升,已知大气压强 $p_{0} = 1.0 \times 10^{5} Pa$ , 水的密度 $ρ = 1.0 \times 10^{3} kg / m^{3}$ , 重力加速度大小 $g = 10 m / s^{2}$ 。

(i) 求在水下 $10 m$ 处气泡内外的压强差;

（ii）忽略水温随水深的变化, 在气泡上升到十分接近水面时, 求气泡的半径与其原来半径之比的近似值。

如图, 两固定的绝缘斜面倾角均为 $θ$ , 上沿相连。两细金属棒 $ab$ （仅标出 a 端 $)$ 和 $cd$ (仅标出 $c$ 端）长度均为 $L$ , 质量分别为 $2 m$ 和 $m$ ; 用两根不可伸长的柔软导线将它们连成闭合回路 abdca, 并通过固定在斜面上沿的两光滑绝缘小定滑轮跨放在斜面上, 使两金属棒水平。右斜面上存在匀强磁场, 磁感应强度大小为 $B$ , 方向垂直于斜面向上，已知两根导线刚好不在磁场中, 回路电阻为 $R$ , 两金属棒与斜面间的动摩擦因数均为 $μ$ , 重力加速度大小为 $g$ , 已知金属棒 $ab$ 匀速下滑。

求：（1）作用在金属棒 $ab$ 上的安培力的大小;

(2) 金属棒运动速度的大小。

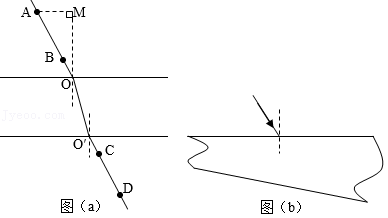
用插针法测量上、下表面平行的玻璃砖的折射率。实验中用A、B两个大头针确定入射光路，C、D两个大头针确定出射光路， $O$ 和 $O'$ 分别是入射点和出射点。如图（a）所示。测得玻璃砖厚度为 $h ＝ 15.0 mm$ ；A到过 $O$ 点的法线 $OM$ 的距离 $AM ＝ 10.0 mm$ ， $M$ 到玻璃砖的距离 $MO ＝ 20.0 mm$ ， $O'$ 到 $OM$ 的距离为 $s ＝ 5.0 mm$ 。

（ⅰ）求玻璃砖的折射率；

（ⅱ）用另一块材料相同，但上下两表面不平行的玻璃砖继续实验，玻璃砖的截面如图（b）所示。光从上表面入射，入射角从 $0$ 逐渐增大，达到 $45 °$ 时，玻璃砖下表面的出射光线恰好消失。求此玻璃砖上下表面的夹角。

试卷网试题网古诗词网作文网范文网