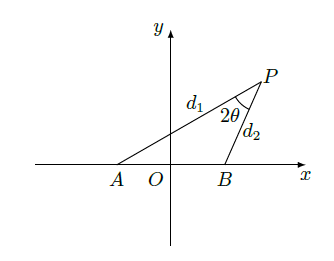
设动点
到点
和
的距离分别为
和
,
,且存在常数
(
,使得
.
(1)证明:动点
的轨迹
为双曲线,并求出
的方程;
(2)过点
作直线交双曲线
的右支于
、
两
点,试确定λ的范围,使
,其中点O为坐标原点.
【2015高考广东,文19】(本小题满分14分)设数列 的前
的前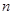 项和为
项和为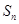 ,
,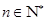 .已知
.已知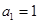 ,
,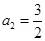 ,
,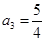 ,且当
,且当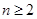
时, .
.
(1)求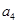 的值;
的值;
(2)证明: 为等比数列;
为等比数列;
(3)求数列 的通项公式.
的通项公式.
【2015高考安徽,文18】已知数列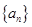 是递增的等比数列,且
是递增的等比数列,且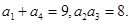
(Ⅰ)求数列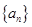 的通项公式;
的通项公式;
(Ⅱ)设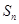 为数列
为数列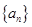 的前n项和,
的前n项和,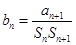 ,求数列
,求数列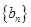 的前n项和
的前n项和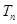 .
.
【2015高考北京,文16】(本小题满分13分)已知等差数列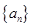 满足
满足 ,
, .
.
(Ⅰ)求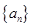 的通项公式;
的通项公式;
(Ⅱ)设等比数列 满足
满足 ,
,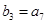 ,问:
,问: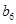 与数列
与数列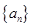 的第几项相等?
的第几项相等?
【2015高考福建,文17】等差数列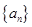 中,
中, ,
,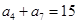 .
.
(Ⅰ)求数列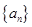 的通项公式;
的通项公式;
(Ⅱ)设 ,求
,求 的值.
的值.
【2015高考天津,文16】(本小题满分13分)△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为 ,
,
(Ⅰ)求a和sinC的值;
(Ⅱ)求 的值.
的值.