、如图所示,在一光滑水平的桌面上,放置一质量为M,宽为L的足够长“U”型框架,其ab部分电阻为R,框架其它部分的电阻不计。垂直框架两边放一质量为m、电阻为R的金属棒cd,它们之间的动摩擦因数为μ,棒通过细线跨过一定滑轮与劲度系数为k 的另一端固定的轻弹簧相连。开始弹簧处于自然状态,框架和棒均静止。现在让框架在大小为2μmg的水平拉力作用下,向右做加速运动,引起棒的运动可看成是缓慢的。水平桌面位于竖直向上的匀强磁场中,磁感应强度为B。
问:(1)框架和棒刚开始运动的瞬间,框架的加速度为多大?
(2)框架最后做匀速运动(棒处于静止状态)时的速度多大?
(3)若框架通过位移S后开始匀速,已知弹簧的弹性势能的表达式为kx2/2(x为弹簧的形变量),则在框架通过位移S的过程中,回路中产生的电热为多少?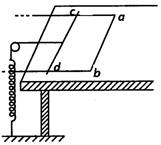
如图所示,光滑水平面上静止放着长L=1.6m,质量为M=3kg的木块(厚度不计),一个质量为m=1kg的小物体放在木板的最右端,m和M之间的动摩擦因数μ=0.1,今对木板施加一水平向右的拉力F,(g取10m/s2)
为使小物体不掉下去,F不能超过多少?
如果F=10N,求小物体所能获得的最大动能?
如果F=10N,要使小物体从木板上掉下去,F作用的时间不能小于多少?
宇航员在一行星上以速度v0竖直上抛一的物体,不计空气阻力,经t秒后落回手中,已知该星球半径为R.求该行星的密度
求该行星的第一宇宙速度.
要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?已知取无穷远处引力势能为零时,物体距星球球心距离r时的引力势能为:
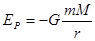 . (G为万有引力常量)
. (G为万有引力常量)
小球在外力作用下,由静止开始从A点出发做匀加速直线运动,到B点时撤去外力,然后,小球冲上竖直平面内固定的光滑圆环,恰能维持在圆环上做圆周运动,到达最高点C后抛出,最后落回到原来的出发点A处,如图所示.试求小球在AB段运动的加速度大小(不计各处摩擦). (g ="10" m/s2)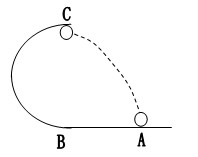
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在 -0.3m ≤ X ≤ -0.2m的长条形范围内存在竖直方向的匀强电场E0;在X ≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T。有一带电量q =+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出, yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为600。g取10m/s2。求: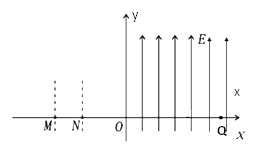
场强E0的大小和方向;
P点的坐标及圆形磁场区的最小半径r;
微粒从进入最小圆形磁场区到击中Q点的运动时间(可以用根号及π等表示)
如图甲所示,在一对平行光滑的金属导轨的上端连接一阻值为R=4 Ω的定值电阻,两导轨在同一平面内.质量为m=0.1 kg,长为L=0.1 m的导体棒ab垂直于导轨,使其从靠近电阻处由静止开始下滑,已知导体棒电阻为r=1 Ω,整个装置处于垂直于导轨平面的匀强磁场中,导体棒下滑过程中加速度a与速度v的关系如图乙所示.(g=10 m/s2).求: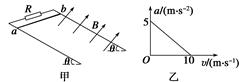
导轨平面与水平面间夹角θ;
磁场的磁感应强度B;
若靠近电阻处到底端距离为20 m,
ab棒在下滑至底端前速度已达10 m/s,
求ab棒下滑的整个过程中,电阻R上产生的焦耳热.