(本题14分)
已知函数 (其中常数a,b∈R),
(其中常数a,b∈R),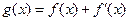 是奇函数.
是奇函数.
(1)求 的表达式;
的表达式;
(2)讨论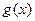 的单调性,并求
的单调性,并求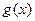 在区间[1,2]上的最大值和最小值.
在区间[1,2]上的最大值和最小值.
正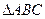 的边长为4,CD是AB边上的高,E、F分别是AC和BC的中点,现将
的边长为4,CD是AB边上的高,E、F分别是AC和BC的中点,现将 沿CD翻折成直二面角
沿CD翻折成直二面角 ,(1)求证:
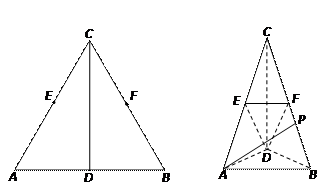
,(1)求证: ;(2)若点P在线段BC上,且BC=3BP,求证
;(2)若点P在线段BC上,且BC=3BP,求证 .
.
已知函数 ,(1)求
,(1)求 的单调区间;(2)若
的单调区间;(2)若 ,求
,求 在区间
在区间 上的最值;
上的最值;
(本小题满分12分)数列 的前n项和为
的前n项和为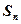 ,且满足
,且满足 ,
,
数列 中,
中,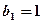 ,且点
,且点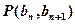 在直线
在直线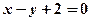 上,
上,
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 , 求
, 求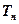 ;
;
(3)设 ,求使得
,求使得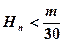 对所有的
对所有的 都成立的最小正整数
都成立的最小正整数 .
.
(本小题满分12) 某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始, 每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(本小题满分12分)解关于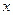 的不等式:
的不等式: (其中
(其中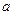
 )
)