某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
15 |
① |
| 第2组 |
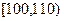 |
② |
0.35 |
| 第3组 |
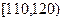 |
20 |
0.20 |
| 第4组 |
 |
20 |
0.20 |
| 第5组 |
 |
10 |
0.10 |
| 合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
已知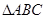 中,a,b, c 为角A,B,C 所对的边,
中,a,b, c 为角A,B,C 所对的边, .
.
(1)求cos A的值;
(2)若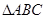 的面积为
的面积为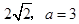 ,求b ,c 的长.
,求b ,c 的长.
设函数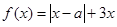 ,其中
,其中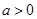 .
.
(1)当 时,求不等式
时,求不等式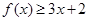 的解集;
的解集;
(2)若不等式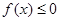 的解集为
的解集为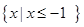 ,求
,求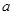 的值.
的值.
已知曲线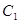 的参数方程为
的参数方程为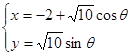 (
(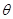 为参数),曲线
为参数),曲线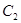 的极坐标方程为
的极坐标方程为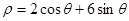 .
.
(1)将曲线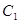 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线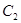 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)曲线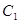 ,
,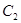 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
如图,A,B,C,D四点在同一圆上,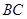 与
与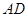 的延长线交于点
的延长线交于点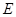 ,点
,点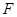 在
在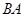 的延长线上.
的延长线上.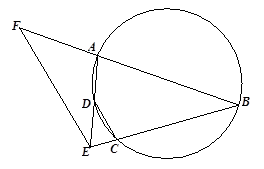
(1)若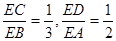 ,求
,求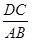 的值;
的值;
(2)若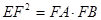 ,证明:
,证明: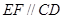 .
.
已知函数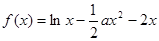 .
.
(1)若函数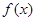 在
在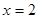 处取得极值,求实数
处取得极值,求实数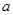 的值;
的值;
(2)若函数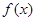 在定义域内单调递增,求实数
在定义域内单调递增,求实数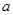 的取值范围;
的取值范围;
(3)当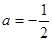 时,关于
时,关于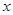 的方程
的方程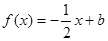 在
在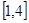 上有两个不相等的实数根,求实数
上有两个不相等的实数根,求实数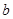 的取值范围.
的取值范围.