(本小题共12分)已知函数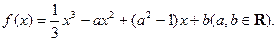
(I)若x=1为 的极值点,求a的值;
的极值点,求a的值;
(II)若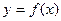 的图象在点(1,
的图象在点(1, )处的切线方程为
)处的切线方程为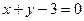 ,求
,求 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
已知数列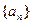 满足
满足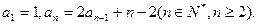
(1)求数列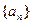 的通项公式;
的通项公式;
(2)设b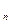 =
=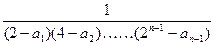 (n∈N
(n∈N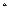 ,n≥2), b
,n≥2), b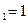 ,求证:b
,求证:b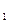 +b
+b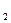 +……+b
+……+b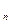 < 3 .
< 3 .
已知F1、F2是椭圆 的两个焦点,O为坐标原点,点P
的两个焦点,O为坐标原点,点P )在椭圆上,线段PF2与y轴的交点M满足
)在椭圆上,线段PF2与y轴的交点M满足 ;
;
(1)求椭圆的标准方程;
(2)⊙O是以F1F2为直径的圆,一直线l: y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当 ,且满足
,且满足 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
直线 与椭圆
与椭圆 交于A、B两点,记△ABO的面积为S.
交于A、B两点,记△ABO的面积为S.
(1)求在k = 0,0 < b < 1的条件下,S的最大值;
(2)当 | AB | = 2,S = 1时,求直线AB的方程.
某集团设资兴办甲、乙两个企业,2005年甲企业获利润32万元,乙企业获利润72万元,以后每年甲企业的利润以上一年的1.5倍递增.而乙企业的利润是上一年利润的 ,预期目标为两企业年利润之和为160万元,以2006年初起.
,预期目标为两企业年利润之和为160万元,以2006年初起.
(1)哪一年两企业获利之和最小,最小值为多少?
(2)经过几年可以达到预期目标?(精确到年)
已知 在曲线
在曲线 上(
上( ),且
),且
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前n项和为Tn,且满足
的前n项和为Tn,且满足 ,试确定b1的值,使得
,试确定b1的值,使得 是等差数列.
是等差数列.