设函数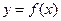 在(
在(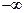 ,+
,+ )内有定义.对于给定的正数K,定义函数
)内有定义.对于给定的正数K,定义函数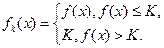 取函数
取函数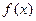 =
=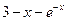 .若对任意的
.若对任意的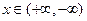 ,恒有
,恒有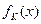 =
=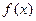 ,则 ( )
,则 ( )
| A.K的最大值为2 | B.K的最小值为2 |
| C.K的最大值为1 | D.K的最小值为1 |
下列有关命题的说法正确的是()
A.命题“若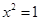 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若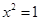 ,则 ,则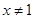 ”. ”. |
B.“ ”是“ ”是“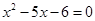 ”的必要不充分条件. ”的必要不充分条件. |
C.命题“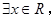 使得 使得 ”的否定是:“ ”的否定是:“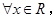 均有 均有 ”. ”. |
D.命题“若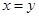 ,则 ,则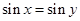 ”的逆否命题为真命题 ”的逆否命题为真命题 |
设集合A={4,5,7,9},B={3,4,7,8,9},全集U = A B,则集合
B,则集合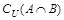 的真子集共有()
的真子集共有()
| A.3个 | B.6个 | C.7个 | D.8个 |
F1,F2是双曲线 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线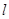 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若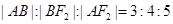 ,则双曲线的离心率是()
,则双曲线的离心率是()
A.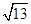 |
B. |
C.2 | D.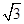 |
对于曲线 ∶
∶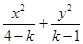 =1,给出下面四个命题:
=1,给出下面四个命题:
(1)曲线 不可能表示椭圆;
不可能表示椭圆;
(2)若曲线 表示焦点在x轴上的椭圆,则1<
表示焦点在x轴上的椭圆,则1<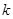 <
< ;
;
(3)若曲线 表示双曲线,则
表示双曲线,则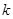 <1或
<1或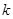 >4;
>4;
(4)当1<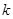 <4时曲线
<4时曲线 表示椭圆,其中正确的是 ()
表示椭圆,其中正确的是 ()
| A.(2)(3) | B.(1)(3) | C.(2)(4) | D.(3)(4) |
已知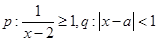 ,若
,若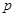 是
是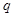 的充分不必要条件,则实数
的充分不必要条件,则实数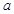 的取值范围为( )
的取值范围为( )
| A.(-∞,3] | B.[2,3] | C.(2,3] | D.(2,3) |