(本小题满分12分)
设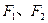 分别为椭圆
分别为椭圆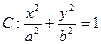 (
( )的左、右焦点,过F2的
)的左、右焦点,过F2的
直线l与椭圆C相交于A、B两点,直线l的倾斜角为600,F1到直线l的
距离为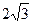 .
.
⑴求椭圆C的焦距;
⑵如果 ,求椭圆C的方程.
,求椭圆C的方程.
如图所示,直三棱柱ABC A1B1C1中,D,E分别是AB,BB1的中点.
A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2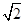 ,求三棱锥C
,求三棱锥C A1DE的体积.
A1DE的体积.
如图,三棱柱ABC A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C= ,求三棱柱ABC
,求三棱柱ABC A1B1C1的体积.
A1B1C1的体积.
如图,四棱锥P ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD= .
.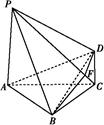
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P BDF的体积.
BDF的体积.
已知函数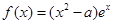 .
.
(Ⅰ)若函数 在
在 上不是单调函数,求实数
上不是单调函数,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,讨论函数
时,讨论函数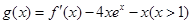 的零点个数.
的零点个数.
设函数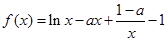 .
.
(Ⅰ)当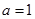 时,求曲线
时,求曲线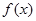 在
在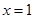 处的切线方程;
处的切线方程;
(Ⅱ)当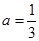 时,求函数
时,求函数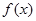 的单调区间;
的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数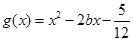 ,若对于
,若对于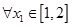 ,
,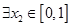 ,使
,使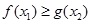 成立,求实数
成立,求实数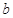 的取值范围.
的取值范围.