(16分) 如图所示，质量m =" 2.0" kg的木块静止在高h =" 1.8" m的水平台上，木块距平台右边缘10 m，木块与平台间的动摩擦因数µ= 0.2。用水平拉力F = 20N拉动木块，当木块运动到水平末端时撤去F。不计空气阻力，g取10m/s2。求：
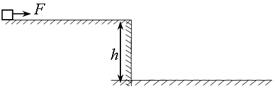
（1）木块离开平台时的速度大小；
（2）木块落地时距平台边缘的水平距离。
为什么目前医院里还没有应用心磁图和脑磁图呢？
如图所示，放在通电螺线管内部中间处的小磁针，静止时N极指向右，试判定电源的正负极.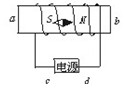
氢原子的核外电子绕原子核按顺时针方向做圆周运动时,设想在原子核处放一小磁针,则小磁针N极指向何方？
有两根外形基本相同的铁条，已知其中一根是永磁体，另一根是普通软铁，单凭视觉是无法将它们区分开的.若不用其他任何器材，如何才能把它们区分开来?
在以坐标原点 O为圆心、半径为 r的圆形区域内，存在磁感应强度大小为 B、方向垂直于纸面向里的匀强磁场，如图所示。一个不计重力的带电粒子从磁场边界与 x轴的交点 A处以速度 v沿－x方向射入磁场，它恰好从磁场边界与 y轴的交点 C处沿+y方向飞出。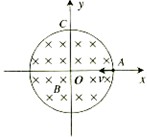
（1）请判断该粒子带何种电荷，并求出其比荷q/m ；
（2）若磁场的方向和所在空间范围不变，而磁感应强度的大小变为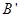
，该粒子仍从 A处以相同的速度射入磁场，但飞出磁场时的速度方向相对于入射方向改变了60°角，求磁感应强度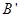多大？此次粒子在磁场中运动所用时间 t是多少？