如图所示,A、B两物体的质量分别为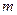 和2
和2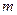 中间用轻质弹簧相连,A、B两物体与水平面间的动摩擦因数均为
中间用轻质弹簧相连,A、B两物体与水平面间的动摩擦因数均为 ,在水平推力F作用下,A、B两物体一起以加速度
,在水平推力F作用下,A、B两物体一起以加速度 向右做匀加速直线运动。当突然撤去推力F的瞬间,则A、B两物体的加速度大小分别为多少?
向右做匀加速直线运动。当突然撤去推力F的瞬间,则A、B两物体的加速度大小分别为多少?
如图所示,ABC为一透明材料 做成的柱形光学元件的横截面,该种材料折射率n=2,AC为一半径为R的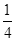 圆弧,D为圆弧面圆心,ABCD构成正方形,在D处有一点光源。若只考虑首次从圆弧AC直接射向AB、BC的光线,从点光源射入圆弧AC的光中,有一部分不能从AB、BC面直接射出,求这部分光照射圆弧AC的弧长。
圆弧,D为圆弧面圆心,ABCD构成正方形,在D处有一点光源。若只考虑首次从圆弧AC直接射向AB、BC的光线,从点光源射入圆弧AC的光中,有一部分不能从AB、BC面直接射出,求这部分光照射圆弧AC的弧长。
如图所示,两根与水平面成θ=30°角的足够长光滑金属导轨平行放置,导轨间距为L=1m,导轨底端接有阻值为0.5W的电阻R,导轨的电阻忽略不计。整个装置处于匀强磁场中,磁场方向垂直于导轨平面斜向上,磁感应强度B=1T。现有一质量为m=0.2 kg、电阻为0.5W的金属棒用细绳通过光滑滑轮与质量为M=0.5 kg的物体相连,细绳与导轨平面平行。将金属棒与M由静止释放,棒沿导轨运动了2 m后开始做匀速运动。运动过程中,棒与导轨始终保持垂直接触。(取重力加速度g=10m/s2)求:
(1)金属棒匀速运动时的速度;
(2)棒从释放到开始匀速运动的过程中,电阻R上产生的焦耳热;
(3)若保持某一大小的磁感应强度B1不变,取不同质量M的物块拉动金属棒,测出金属棒相应的做匀速运动的v值,得到实验图像如图所示,请根据图中的数据计算出此时的B1;
改变磁感应强度的大小为B2,B2=2B1,其他条件不变,请在坐标图上画出相应的v—M图线,并请说明图线与M轴的交点的物理意义。
如图所示,长为l、内壁光滑的直管与水平地面成30°角固定放置,上端管口水平,且水平部分管口长度忽略不计,质量为m的小球可在直管内自由滑动,用一根轻质光滑细线将小球与另一质量为M的物块相连,M=3m。开始时小球固定于管底,物块悬挂于管口,小球、物块均可视为质点。将小球释放,小球在管口的转向过程中速率不变。试求:
(1)物块落地前瞬间的速度大小;
(2)小球做平抛运动的水平位移;(M落地后绳子一直松弛)
(3)有同学认为,若取M=km,则k足够大时,能使小球平抛运动水平位移的大小最大达到绳长l,请通过计算判断这种说法是否正确。
玻璃板生产线上,宽9 m的成型玻璃板以2 m/s的速度连续不断地向前行进,在切割工序处,金刚钻的走刀速度为10 m/s,为了使割下的玻璃板都成规定尺寸的矩形,金刚钻割刀的轨道应如何控制?切割一次的时间多长?
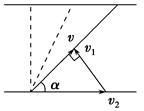
有一小船正在渡河,如图所示.在离对岸30 m时,其下游40 m处有一危险水域.假若水流速度为5 m/s,为了使小船在危险水域之前到达对岸,则小船从现在起相对于静水的最小速度应是多大?