已知各项均为正数的数列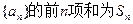 ,
,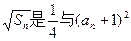 的等比中项。
的等比中项。
(1)求证:数列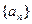 是等差数列;(2)若
是等差数列;(2)若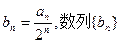 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
定义在 上的函数
上的函数 对任意
对任意 都有
都有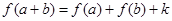 (
( 为常数).
为常数).
(1)判断 为何值时
为何值时 为奇函数,并证明;
为奇函数,并证明;
(2)设 ,
, 是
是 上的增函数,且
上的增函数,且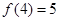 ,若不等式
,若不等式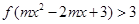 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,四棱锥 中,侧面
中,侧面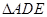 是等边三角形,在底面等腰梯形
是等边三角形,在底面等腰梯形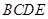 中,
中, ,
, ,
,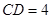 ,
, ,
, 为
为 的中点,
的中点, 为
为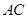 的中点,
的中点,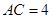 .
.
(1)求证:平面 平面
平面 ;
;
(2)求证: 平面
平面 .
.
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到频率分布表如下:

(1)求表中 的值及分数在
的值及分数在 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
已知二次函数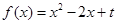 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.
(1)求实数t的取值范围;
(2)当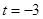 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;
(3)过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点,求四边形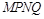 的面积的最大值。
的面积的最大值。
在数列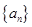 中,已知
中,已知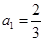 ,
,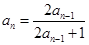 .
.
(1)求 、
、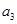 并判断
并判断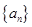 能否为等差或等比数列;
能否为等差或等比数列;
(2)令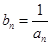 ,求证:
,求证: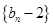 为等比数列;
为等比数列;
(3)求数列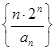 的前n项和
的前n项和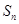 .
.