(本题12分)如图,已知△ABC是边长为1的正三角形,M、N分别是
边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(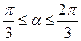 )
)
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数
(2)求y=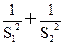 的最大值与最小值
的最大值与最小值
在 中,内角
中,内角 所对的边长分别为
所对的边长分别为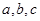 ,
,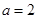 ,
,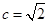 ,
,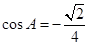 .
.
求sinC和b的值.
已知函数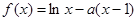 ,
,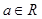 .
.
(I)讨论函数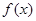 的单调性;
的单调性;
(Ⅱ)当 时,
时,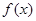 ≤
≤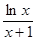 恒成立,求
恒成立,求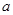 的取值范围.
的取值范围.
如图,在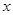 轴上方有一段曲线弧
轴上方有一段曲线弧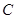 ,其端点
,其端点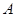 、
、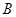 在
在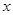 轴上(但不属于
轴上(但不属于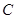 ),对
),对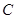 上任一点
上任一点 及点
及点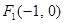 ,
,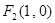 ,满足:
,满足: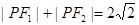 .直线
.直线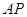 ,
,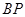 分别交直线
分别交直线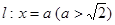 于
于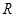 ,
, 两点.
两点.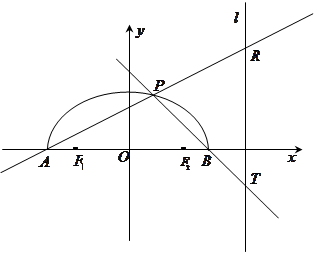
(Ⅰ)求曲线弧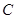 的方程;
的方程;
(Ⅱ)求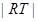 的最小值(用
的最小值(用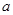 表示);
表示);
小波以游戏方式决定参加学校合唱团还是参加学校排球队.游戏规则为:以O为起点,再从 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为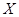 .若
.若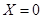 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.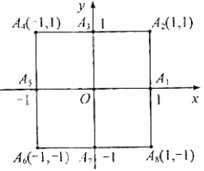
(I)求小波参加学校合唱团的概率;
(II)求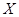 的分布列和数学期望.
的分布列和数学期望.
在平面直角坐标系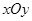 中,直线l与抛物线
中,直线l与抛物线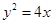 相交于不同的两点A,B.
相交于不同的两点A,B.
(I)如果直线l过抛物线的焦点,求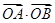 的值;
的值;
(II)如果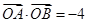 ,证明直线l必过一定点,并求出该定点坐标.
,证明直线l必过一定点,并求出该定点坐标.