(本小题满分13分)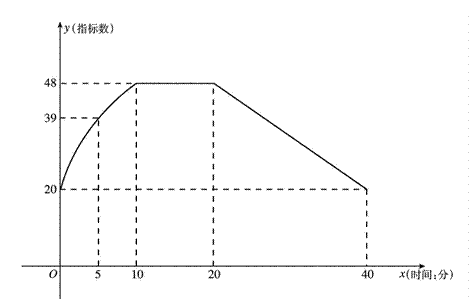
(本小题满分12分)通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散. 学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中). 当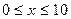 时,图象是抛物线的一部分,当
时,图象是抛物线的一部分,当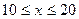 和
和 时,图象是线段.
时,图象是线段.
(1)当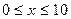 时,求注意力指标数y与时间x的函数关系式;
时,求注意力指标数y与时间x的函数关系式;
(2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
(本小题满分12分)
如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图.已知 ,侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.
,侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.
(Ⅰ)求该几何体的体积;
(Ⅱ)求二面角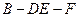 的余弦值.
的余弦值.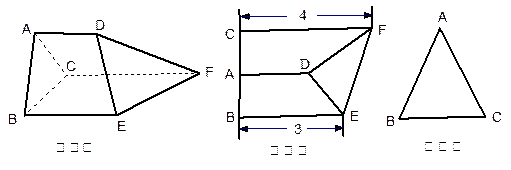
(本小题满分12分)
某篮球职业联赛的总决赛在甲队与乙队间角逐,采用五局三胜制,即若一队先胜三场,则此队获胜,比赛结束,因两队实力相当,每场比赛获胜的可能性相等,据以往资料统计,第一场比赛组织者可获门票收入30万元,以后每场比赛门票收入都比上一场增加10万元,问:
⑴组织者在此次总决赛中获得门票收入不少于180万元的概率是多少?
⑵用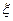 表示组织者在此次总决赛中的门票收入,求
表示组织者在此次总决赛中的门票收入,求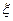 的数学期望?
的数学期望?
(本小题满分12分)
已知函数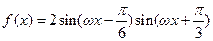 (其中
(其中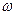 为正常数,
为正常数,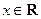 )的最小正周期为
)的最小正周期为 .
.
(1)求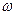 的值;
的值;
(2)在△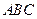 中,若
中,若 ,且
,且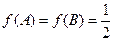 ,求
,求 .
.
在各项均为正数的数列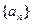 中,前
中,前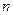 项和
项和 满足
满足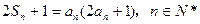 。
。
(1)证明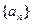 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前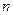 项和的公式;
项和的公式;
(2)在平面直角坐标系 面上,设点
面上,设点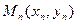 满足
满足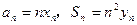 ,且点
,且点 在直线
在直线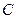 上,
上, 中最高点为
中最高点为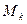 ,若称直线
,若称直线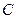 与
与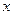 轴、直线
轴、直线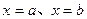 所围成的图形的面积为直线
所围成的图形的面积为直线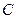 在区间
在区间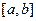 上的面积,试求直线
上的面积,试求直线 在区间
在区间 上的面积;
上的面积;
(3)求出圆心在直线 上的圆,使得点列
上的圆,使得点列 中任何一个点都在该圆内部
中任何一个点都在该圆内部