在纳米技术中需要移动或修补原子,必须使在不停地做热运动(速率约几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间,为此已发明了“激光致冷”的技术。若把原子和入射光子分别类比为一辆小车和一个小球,则“激光致冷”与下述的力学模型很相似。
一辆质量为m的小车(一侧固定一轻弹簧),如图所示以速度V0水平向右运动,一个动量大小为p,质量可以忽略的小球水平向左射入小车并压缩弹簧至最短,接着被锁定一段时间△T,再解除锁定使小球以大小相同的动量P水平向右弹出,紧接着不断重复上述过程,最终小车将停下来。设地面和车厢均为光滑,除锁定时间△T外,不计小球在小车上运动和弹簧压缩、伸长的时间。求:
(1)小球第一次入射后再弹出时,小车的速度的大小和这一过程中小车动能的减少量。
(2)从小球第一次入射开始到小车停止运动所经历的时间。
如图所示,质量为2 kg的直角三棱柱A放在水平地面上,三棱柱的斜面是光滑的,且斜面倾角 为37°.质量为1 kg的光滑球放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱的支持力和摩擦力各为多少?(g=10m/s
为37°.质量为1 kg的光滑球放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱的支持力和摩擦力各为多少?(g=10m/s sin 37°
sin 37° cos 37°
cos 37°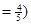

静电喷漆技术具有效率高、浪费少、质量好、有益于健康等优点,其装置可简化如图。 、
、 为水平放置的间距
为水平放置的间距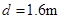 的两块足够大的平行金属板,两板间有方向由
的两块足够大的平行金属板,两板间有方向由 指向
指向 的匀强电场,场强为
的匀强电场,场强为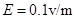 。在
。在 板的中央放置一个安全接地的静电油漆喷枪
板的中央放置一个安全接地的静电油漆喷枪 ,油漆喷枪可向各个方向均匀地喷出初速度大小均为
,油漆喷枪可向各个方向均匀地喷出初速度大小均为 的油漆微粒,已知油漆微粒的质量均为
的油漆微粒,已知油漆微粒的质量均为 、电荷量均为
、电荷量均为 ,不计油漆微粒间的相互作用、油漆微粒带电对板间电场和磁场的影响及空气阻力,重力加速度
,不计油漆微粒间的相互作用、油漆微粒带电对板间电场和磁场的影响及空气阻力,重力加速度 。求:
。求:
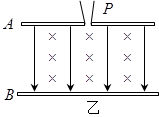
(1)油漆微粒落在 板上所形成的图形面积;
板上所形成的图形面积;
(2)若让 、
、 两板间的电场反向,并在两板间加垂直于纸面向里的匀强磁场,磁感应强度
两板间的电场反向,并在两板间加垂直于纸面向里的匀强磁场,磁感应强度 ,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变。
,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变。 板被油漆微粒打中的区域的长度;
板被油漆微粒打中的区域的长度;
(3) 在满足(2)的情况下,打中 板的油漆微粒中,在磁场中运动的最短时间。
板的油漆微粒中,在磁场中运动的最短时间。
如图所示,在光滑水平地面上有一固定的挡板,挡板左端固定一个轻弹簧。现有一质量M=3kg,长L=4m的小车AB(其中 为小车的中点,
为小车的中点, 部分粗糙,
部分粗糙, 部分光滑)一质量为m=1kg的小物块(可视为质点),放在车的最左端,车和小物块一起以
部分光滑)一质量为m=1kg的小物块(可视为质点),放在车的最左端,车和小物块一起以 4m/s的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车
4m/s的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车 部分的长度大于弹簧的自然长度,弹簧始终处于弹性限度内,小物块与车
部分的长度大于弹簧的自然长度,弹簧始终处于弹性限度内,小物块与车 部分之间的动摩擦因数为
部分之间的动摩擦因数为 0.3,重力加速度
0.3,重力加速度 。求:
。求:


(1)小物块和弹簧相互作用的过程中,弹簧具有的最大弹性势能;
(2)小物块和弹簧相互作用的过程中,弹簧对小物块的冲量;
(3)小物块最终停在小车上的位置距 端多远。
端多远。
如图所示,  和
和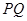 为固定在绝缘水平面上两平行光滑金属导轨,导轨左端
为固定在绝缘水平面上两平行光滑金属导轨,导轨左端 间接有阻值为
间接有阻值为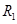 =
= 导线;导轨右端接有与水平轨道相切、半径
导线;导轨右端接有与水平轨道相切、半径 内壁光滑的半圆金属轨道。导轨间距
内壁光滑的半圆金属轨道。导轨间距 ,电阻不计。导轨所在平面
,电阻不计。导轨所在平面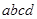 区域内有竖直向上
区域内有竖直向上 的匀强磁场。导轨上长度也为
的匀强磁场。导轨上长度也为 、质量
、质量 、电阻
、电阻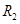 =
= 的金属棒
的金属棒 以
以 =
= 速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度
速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度 =
=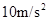 。求:
。求: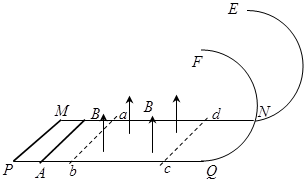
(1)金属棒 刚滑出磁场右边界
刚滑出磁场右边界 时的速度
时的速度 的大小;
的大小;
(2)金属棒滑过磁场区的过程中,导线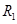 中产生的热量
中产生的热量 。
。
如图所示,是磁流体动力发电机的工作原理图.一个水平放置的上下、前后封闭的矩形塑料管,其宽度为a,高度为b,其内充满电阻率为ρ的水银,由涡轮机产生的压强差p使得这个流体具有恒定的流速v0.管道的前后两个侧面上各有长为L的由铜组成的面,实际流体的运动非常复杂,为简化起见作如下假设: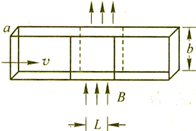
a.尽管流体有粘滞性,但整个横截面上的速度均匀;
b.流体的速度总是与作用在其上的合外力成正比;
c.导体的电阻:R=ρl/S,其中ρ、l和S分别为导体的电阻率、长度和横截面积;
d.流体不可压缩.
若由铜组成的前后两个侧面外部短路,一个竖直向上的匀强磁场只加在这两个铜面之间的区域,磁感强度为B(如图).
(1)写出加磁场后,两个铜面之间区域的电阻R的表达式
(2)加磁场后,假设新的稳定速度为v,写出流体所受的磁场力F与v关系式,指出F的方向
(3)写出加磁场后流体新的稳定速度v的表达式(用v0、p、L、B、ρ表示);
(4)为使速度增加到原来的值v0,涡轮机的功率必须增加,写出功率增加量的表达式(用v0、a、b、L、B和ρ表示)。