(选修模块3—5)
(1)下列说法正确的是
| A.康普顿效应进一步证实了光的波动特性 |
| B.为了解释黑体辐射规律,普朗克提出电磁辐射的能量的量子化 |
| C.经典物理学不能解释原子的稳定性和原子光谱的分立特征 |
| D.天然放射性元素的半衰期与环境的温度有关 |
(2)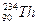 是不稳定的,能自发地发生衰变。
是不稳定的,能自发地发生衰变。
①完成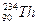 衰变反
衰变反 应方程
应方程 。
。
②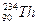 衰变为
衰变为 ,共经过 次
,共经过 次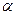 衰变, 次
衰变, 次 衰变。
衰变。
(3)氢原子的能级如图所示,有一群处于n=4能级的氢原子。如果原子n=2向n=1跃迁所发生的光正好使某种金属材料产生光电效应,则:
①这群氢原子发出的光谱中共有几条谱线能使该金属产生光电效应?
②从能级n=4向n=1发出的光照射该金属材料,所产生的光电子的最大初动能为多少?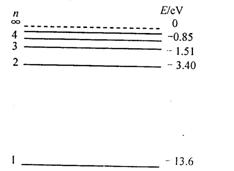
在纳米技术中需要移动或修补原子,必须使在不停地做热运动(速率约几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间,为此已发明了“激光致冷”的技术。若把原子和入射光子分别类比为一辆小车和一个小球,则“激光致冷”与下述的力学模型很相似。
一辆质量为m的小车(一侧固定一轻弹簧),如图所示以速度V0水平向右运动,一个动量大小为p,质量可以忽略的小球水平向左射入小车并压缩弹簧至最短,接着被锁定一段时间△T,再解除锁定使小球以大小相同的动量P水平向右弹出,紧接着不断重复上述过程,最终小车将停下来。设地面和车厢均为光滑,除锁定时间△T外,不计小球在小车上运动和弹簧压缩、伸长的时间。求:
(1)小球第一次入射后再弹出时,小车的速度的大小和这一过程中小车动能的减少量。
(2)从小球第一次入射开始到小车停止运动所经历的时间。
如图所示,足够长的光滑平台固定在水平地面上,平台中间放有小物体A和B,两者彼此接触.A的上表面是半径为R的半圆形轨道,轨道顶端距台面的高度为h处,有一个小物体C,A、B、C的质量均为m,在系统静止时释放C,已知在运动过程中 ,A、C始终接触,试求:
,A、C始终接触,试求:
(1)物体A和B刚分离时,B的速度.
(2)物体A和B分离后,C所能达到的距台面的最大高度.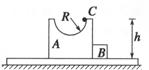
如图所示,两足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定为I.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求:
(1)磁感应强度的大小B;
(2)电流稳定后,导体棒运动速度的大小v;
(3)流经电流表电流的最大值Im.
已知氢原子处于基态时,原子的能量E1=-13.6 eV,电子的轨道半径为r1=0.53×10-10 m;而量子数为n的能级值为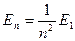 ,半径
,半径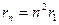 .试问(结果保留两位有效数字):
.试问(结果保留两位有效数字):
(1)若要使处于n=2的激发态的氢原子电离,至少要用频率多大的光照射氢原子?
(2)氢原子处于n=2能级时,电子在轨道上运动的动能和电子的电势能各为多少?
(静电力常量k=9×109 N·m2/C2,电子电荷量e=1.6×10-19 C,普朗克常量h=6.63× 10-34 J·s)
10-34 J·s)
地球的质量M=5.98×1024kg,地球半径R=6370km,引力常量G=6.67×10-11Nm2/kg2,一颗绕地做圆周运动的卫星环绕速度为v=2100m/s,求:
(1)用题中的已知量表示此卫星距地面高度h的表达式
(2)此高度的数值为多少?(保留3位有效数字)