(本小题满分12分)
在如图所示的空间几何体中,平面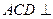 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在 的平分线上。
的平分线上。
(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积。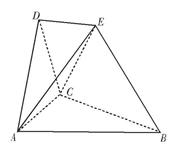
函数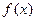 的定义域为
的定义域为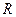 ,并满足以下三个条件:(i)对任意
,并满足以下三个条件:(i)对任意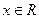 ,有
,有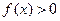 ;
;
(ii)对任意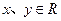 ,有
,有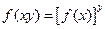 ;(iii)
;(iii)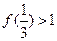 。
。
(1) 求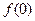 的值;
的值;
(2)求证: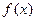 在
在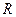 上是单调增函数;
上是单调增函数;
(3)若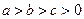 ,且
,且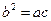 ,求证:
,求证: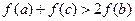 。
。
已知函数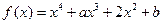 (
(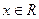 ),其中
),其中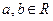 .
.
(Ⅰ)当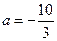 ,
,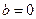 时,求函数
时,求函数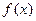 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若函数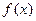 仅在
仅在 处有极值,求实数
处有极值,求实数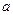 的取值范围;
的取值范围;
(Ⅲ)若对于任意的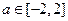 ,不等式
,不等式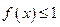 在
在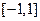 上恒成立,求实数
上恒成立,求实数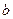 的取值范围.
的取值范围.
已知二次函数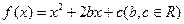 。(1)若
。(1)若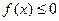 的解集
的解集
为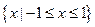 ,求实数
,求实数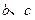 的值;(2)若
的值;(2)若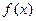 满足
满足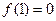 ,且关于
,且关于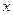 的方程
的方程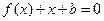 的两个实根分别在区间
的两个实根分别在区间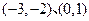 内,求实数
内,求实数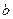 的取值范围。
的取值范围。
命题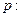 关于
关于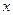 的不等式
的不等式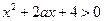 对一切
对一切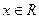 恒成立,
恒成立,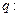 函
函
数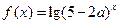 是增函数,若
是增函数,若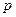 或
或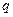 为真命题,
为真命题,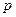 且
且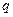 为假命题,求实数
为假命题,求实数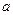 的取值范
的取值范
围。
已知函数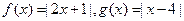 。(1)求不等式
。(1)求不等式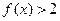 的解
的解
集;(2)若不等式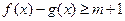 的解集为R,求实数m的取值范围。
的解集为R,求实数m的取值范围。