(本小题满分10分)
已知四棱锥P—ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点。
(I)求AC与PB所 成角的余弦值;
成角的余弦值;
(II)求面AMC与面BMC所成二面角的余弦值的大小。
(本小题满分12分)已知函数
 的最小正周期为
的最小正周期为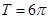 ,且
,且 .
.
(1)求 的表达式;
的表达式;
(2)设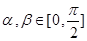 ,
, ,
, ,求
,求 的值.
的值.
(本小题满分14分)已知 ,函数
,函数 =
= .
.
(1)记 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的表达式;
的表达式;
(2)是否存在 ,使函数
,使函数 在区间
在区间 内的图象上存在两点,在该两点处的切线互相垂直?若存在,求
内的图象上存在两点,在该两点处的切线互相垂直?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分14分)在直角坐标系 中,曲线
中,曲线 上的点均在圆
上的点均在圆 外,且对
外,且对 上任意一点
上任意一点 ,
, 到直线
到直线 的距离等于该点与圆
的距离等于该点与圆 上点的距离的最小值.
上点的距离的最小值.
(1)求曲线 的方程;
的方程;
(2)设 为圆
为圆 外一点,过
外一点,过 作圆
作圆 的两条切线,分别与曲线
的两条切线,分别与曲线 相交于点
相交于点 和
和 .证明:当
.证明:当 在直线
在直线 上运动时,四点
上运动时,四点
 的纵坐标之积为定值.
的纵坐标之积为定值.
(本小题满分14分)已知数列 的前
的前 项和为
项和为 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,
, =
= +
+ +
+ + +
+ + .试比较
.试比较 与
与 的大小.
的大小.
(本小题满分14分)如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,平面
,平面 ⊥底面
⊥底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 上的点,
上的点, ,
, ,
, .
.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)若二面角 为
为 ,设
,设 ,试确定
,试确定  的值.
的值.