(本小题满分15分)设椭圆C: (
(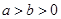 ),
), ,
, 为左、右焦点,
为左、右焦点, 为短轴端点,且
为短轴端点,且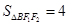 ,离心率为
,离心率为 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆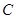 的方程;
的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆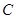 恒有两个交点
恒有两个交点 、
、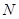 ,且满足
,且满足 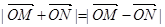 ?若存在,求出该圆的方程,若不存在,说明理由.
?若存在,求出该圆的方程,若不存在,说明理由.
已知直线l与直线 的倾斜角相等,并且与两坐标轴围成的三角形面积等于24,求直线l的方程.
的倾斜角相等,并且与两坐标轴围成的三角形面积等于24,求直线l的方程.
已知圆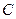 过点
过点 ,且与圆
,且与圆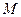 :
: 关于直线
关于直线 对称.
对称.
(Ⅰ)求圆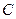 的方程;
的方程;
(Ⅱ)设 为圆
为圆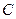 上的一个动点,求
上的一个动点,求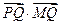 的最小值;
的最小值;
(Ⅲ)过点 作两条相异直线分别与圆
作两条相异直线分别与圆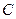 相交于
相交于 ,且直线
,且直线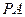 和直线
和直线 的倾斜角互补,
的倾斜角互补, 为坐标原点,试判断直线
为坐标原点,试判断直线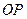 和
和 是否平行?请说明理由.
是否平行?请说明理由.
已知定义域为 的函数
的函数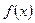 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的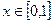 ,总有
,总有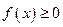 ;②
;② ;③若
;③若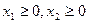 且
且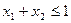 ,则有
,则有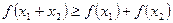 成立,则称
成立,则称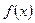 为“友谊函数”.
为“友谊函数”.
(Ⅰ)若已知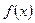 为“友谊函数”,求
为“友谊函数”,求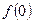 的值;
的值;
(Ⅱ)函数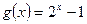 在区间
在区间 上是否为“友谊函数”?并给出理由;
上是否为“友谊函数”?并给出理由;
(Ⅲ)已知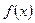 为“友谊函数”,且
为“友谊函数”,且 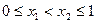 ,求证:
,求证: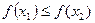 .
.
如图,三棱锥A—BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
(Ⅰ)求证:DM//平面APC;
|
(Ⅱ)求 证:平面ABC⊥平面APC;
(Ⅲ)若BC=4,AB=20,求三棱锥D—BCM的体积.已知函数 ,其中
,其中 .
.
(Ⅰ)若 的单调增区间是
的单调增区间是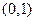 ,求m的值;
,求m的值;
(Ⅱ)当 时,函数
时,函数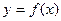 的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
的图象上任意一点的切线斜率恒大于3m,求m的取值范围.