已知函数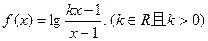 。
。
(1)求函数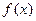 的定义域;
的定义域;
(2)若函数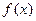 在[10,+∞)上单调递增,求k的取值范围。
在[10,+∞)上单调递增,求k的取值范围。
如图,底面△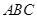 为正三角形的直三棱柱
为正三角形的直三棱柱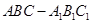 中,
中,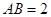 ,
,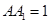 ,
,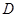 是
是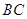 的中点,点
的中点,点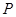 在平面
在平面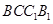 内,
内,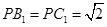 .
. 
(Ⅰ)求证: ;
;
(Ⅱ)求证: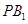 ∥平面
∥平面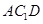 ;
;
(Ⅲ)求二面角 的大小.
的大小.
在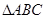 中,
中,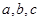 分别为内角
分别为内角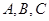 的对边,且
的对边,且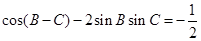 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若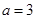 ,
,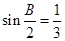 ,求边
,求边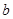 的长.
的长.
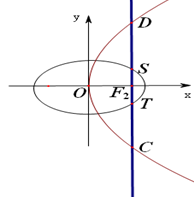
如图,椭圆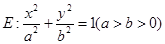 的右焦点
的右焦点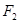 与抛物线
与抛物线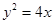 的焦点重合,过
的焦点重合,过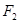 作与
作与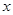 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于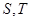 ,而与抛物线交于
,而与抛物线交于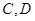 两点,且
两点,且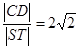 .
.
(Ⅰ)求椭圆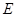 的方程;
的方程;
(Ⅱ)若过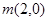 的直线与椭圆
的直线与椭圆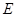 相交于两点
相交于两点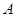 和
和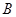 ,
,
设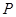 为椭圆
为椭圆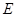 上一点,且满足
上一点,且满足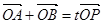 (
(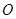 为坐标原点),求实数
为坐标原点),求实数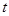 的取值范围.
的取值范围.
已知函数 ,且
,且 。
。
(1)若函数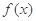 在
在 处的切线与
处的切线与 轴垂直,求
轴垂直,求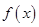 的极值。
的极值。
(2)若函数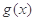 在
在 ,求实数a的值。
,求实数a的值。
如图所示,已知AC ⊥平面CDE, BD ∥AC ,  为等边三角形,F为ED边上的中点,且
为等边三角形,F为ED边上的中点,且 ,
,
(Ⅰ)求证:CF∥面ABE;
(Ⅱ)求证:面ABE ⊥平面BDE;
(Ⅲ)求该几何体ABECD的体积。