已知函数 .
.
(Ⅰ)当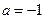 时,求曲线
时,求曲线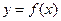 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,讨论
时,讨论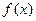 的单调性.
的单调性.
知抛物线C:y2=4x,若椭圆左焦点及相应的准线与抛物线C的焦点F及准线l分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
已知P、Q是椭圆C: 上的两个动点,
上的两个动点, 是椭圆上一定点,
是椭圆上一定点, 是其左焦点,且|PF|、|MF|、|QF|成等差数列。
是其左焦点,且|PF|、|MF|、|QF|成等差数列。
求证:线段PQ的垂直平分线经过一个定点A;
已知点 和
和 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线 交于D、E两点,求线段DE的长.
交于D、E两点,求线段DE的长.
已知椭圆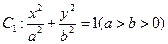 与直线
与直线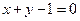 相交于两点
相交于两点 .
.
(1)当椭圆的半焦距 ,且
,且 成等差数列时,求椭圆的方程;
成等差数列时,求椭圆的方程;
(2)在(1)的条件下,求弦 的长度
的长度 ;
;
已知点A、B的坐标分别是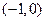 ,
,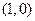 .直线
.直线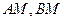 相交于点M,且它们的斜率之积为-2.
相交于点M,且它们的斜率之积为-2.
(Ⅰ)求动点M的轨迹方程;
(Ⅱ)若过点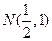 的直线
的直线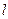 交动点M的轨迹于C、D两点, 且N为线段CD的中点,求直线
交动点M的轨迹于C、D两点, 且N为线段CD的中点,求直线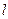 的方程.
的方程.