(本小题满分12分,(Ⅰ)小题5分,(Ⅱ)小题7分)
设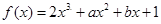 的导数为
的导数为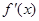 ,若函数
,若函数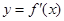 的图像关于直线
的图像关于直线 对称,且
对称,且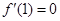 .
.
(Ⅰ)求实数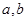 的值(Ⅱ)求函数
的值(Ⅱ)求函数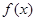 的极值
的极值
(本小题满分10分)已知M(-2,0),N(2,0),求以MN为斜边的直角三角形顶点P的轨迹方程.
已知椭圆
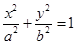 (
( )的半焦距为
)的半焦距为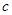 ,原点
,原点 到经过两点
到经过两点 ,
, 的直线的距离为
的直线的距离为 .
.
(Ⅰ)求椭圆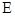 的离心率;
的离心率;
(Ⅱ)如图, 是圆
是圆
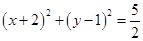 的一条直径,若椭圆
的一条直径,若椭圆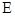 经过
经过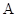 ,
, 两点,求椭圆
两点,求椭圆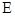 的方程.
的方程.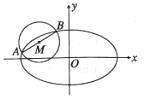
已知点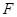 为抛物线
为抛物线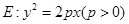 的焦点,点
的焦点,点 在抛物线
在抛物线 上,且
上,且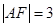 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)已知点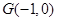 ,延长
,延长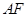 交抛物线
交抛物线 于点
于点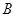 ,证明:以点
,证明:以点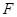 为圆心且与直线
为圆心且与直线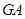 相切的圆,必与直线
相切的圆,必与直线 相切.
相切.
已知二次函数 (
(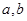 为常数且
为常数且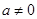 )满足
)满足 且方程
且方程 有等根.
有等根.
(1)求 的解析式;
的解析式;
(2)设 的反函数为
的反函数为 若
若 对
对 恒成立,求实数
恒成立,求实数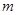 的取值范围.
的取值范围.
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC= ,
,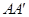 =1,点M、N分别为
=1,点M、N分别为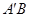 和
和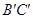 的中点.
的中点.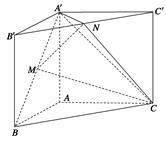
(Ⅰ)证明: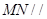 平面
平面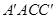 ;
;
(Ⅱ)求三棱锥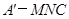 的体积
的体积