已知椭圆
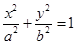 (
( )的半焦距为
)的半焦距为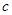 ,原点
,原点 到经过两点
到经过两点 ,
, 的直线的距离为
的直线的距离为 .
.
(Ⅰ)求椭圆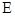 的离心率;
的离心率;
(Ⅱ)如图, 是圆
是圆
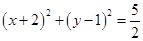 的一条直径,若椭圆
的一条直径,若椭圆 经过
经过 ,
, 两点,求椭圆
两点,求椭圆 的方程.
的方程.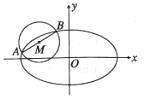
.(12分)在直角坐标系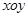 中,以
中,以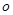 为极点,
为极点,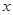 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线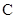 的极坐标方程为
的极坐标方程为 ,
,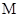 、
、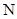 分别为曲线
分别为曲线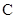 与
与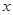 轴,
轴,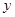 轴的交点。
轴的交点。
(1)写出曲线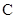 的直角坐标方程,并求
的直角坐标方程,并求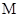 、
、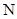 的极坐标;
的极坐标;
(2)设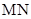 中点为
中点为 ,求直线
,求直线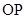 的极坐标方程。
的极坐标方程。
(12分)如图,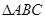 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E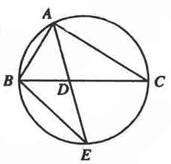
(I)证明: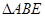

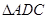
(II)若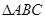 的面积
的面积 ,求
,求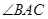 的大小。
的大小。
.(12分)设 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量 的期望
的期望 与方差
与方差 .
.
| ξ |
-1 |
0 |
1 |
| P |
 |
1-2q[ |
q2 |
.(12分)已知 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;
(2)求展开式中系数最大的项.
(12分) 一盒中装有分别标记着1,2,3,4的4个小球,每次从袋中取出一只球,设每只小球被取出的可能性相同.
(1)若每次取出的球不放回盒中,现连续取三次球,求恰好第三次取出的球的标号为最大数字的球的概率;
(2)若每次取出的球放回盒中,然后再取出一只球,现连续取三次球,这三次取出的球中标号最大数字为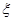 ,求
,求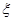 的分布列与数学期望.
的分布列与数学期望.